Polynome mit mehreren Veränderlichen
Der Wert von Polynomen einer Variablen lässt sich vorteilhaft mittels
Hornerschema berechnen.
Eine entsprechende Verallgemeinerung für "dimarg" Veränderliche
erfolgt geordnet nach Basispotenzen für Grad 0, 1,...,n.
Der Übergang von Grad k zu k+1 erfordert jeweils für jede neue Basispotenz
nur die Multiplikation eines geeigneten Partners des k-ten Grades und einer
Grundfunktion x(i). Dabei wird innerhalb k+1 lexikografisch vorgegangen. Diese
beiden Regeln führen zwangsläufig zur bestehenden Form von
"hornarg.f". Man erhält so
Grad 0 : Basispotenz 1, Grad 1 : Basispotenzen
x(1), x(2), ..., x(dimarg) usw. Bei den höheren Graden ergeben sich Produkte
der Form
(x(1)^e(1))*(x(2)^e(2))*...*(x(dimarg)^e(dimarg)) für einen Basispotenzgrad
n=e(1)+e(2)+...+e(dimarg) .
Ein Beispiel für dimarg=8 und n=9 wäre x1^3*x7*x8^5. Für n=9 und dimarg 8 gibt
es übrigens insgesamt 24310 Basispotenzen. Um eine Funktion mittels Polynom mit
8 Variablen und dem Grad 9 darzustellen, wäre daher ein Gleichungssystem vom
Format 24310x24311 zu lösen!
Im begleitenden Fortran-Programm werden mehrere Beispiele angeführt. Als erstes
die Darstellung einer Übersicht der Anzahl von Basispotenzen
dimfn (n,dimarg) in einer Tabelle für n=0, 1, ..., 30
und dimarg=1, 2, ..., 9 .
Dabei ergibte sich dimfn (n,dimarg)
als Summe aller Basispotenzen mit Grad ≤ n.
Im zweiten Teil wird bereits das hauptsächliche Ziel dieser Arbeit angesprochen
- Approximation einer gegebenen Punktmenge.
Dabei wird keine Kenntnis einer zu Grunde liegenden Ursache vorausgesetzt für
eine gegebene Gruppierung in dimarg+1 jeweils zusammen gehörender Daten. Um
einen Überblick zu gewinnen, sind mehrere erste einfache Darstellungen der
Punktmenge hilfreich. Hier ein Beispiel:

Wie viele ähnliche Abbildungen mit jeweils drei Komponenten sind möglich? Und welche Erkenntnisse sind so zu
gewinnen?
Bei dimarg+1 Daten per Gruppierung wird ein Element die gesuchte Funktion und
dimarg Elemente ihr Argument sein. Die Anzahl unterschiedlicher Darstellungen
ergibt sich zu (dimarg+1)!/(dimarg-2)! , dimarg>1.
Zuerst den Index der Funktion ermitteln. Dabei muss ein Bild entsteht, wo ein
möglichst großer Bereich einen erkennbar eindeutigen Verlauf des
approximierenden Polynoms zeigt.
Ein derartiger Index existiert nicht immer. Das kann evtl. doch mittels
geeigneter Transformation der Punktmenge erreicht werden (jedoch nicht hier).
Im betrachteten Beispiel hat die Funktion den Index 3. So bleiben von
ursprünglich 6 Bildern noch 2 zu untersuchen. Im vorliegenden Fall
unterscheiden sich die Bilder bei Austausch der Indizes 1 und 2 nicht. Sehr
günstig.
Allerdings gibt es keine Hoffnung, mit Polynomen in x1,x2
ein brauchbares Resultat zu erzielen. Man sieht aber deutlich, wie periodisch
in beiden Variablen x1,x2 die Punkte angeordnet sind.
Ein Ersatz von x1 durch die Grundfunktion sin(x1) und von x2 durch sin(x2)
führt bereits für n=40 zu folgenden Resultaten:
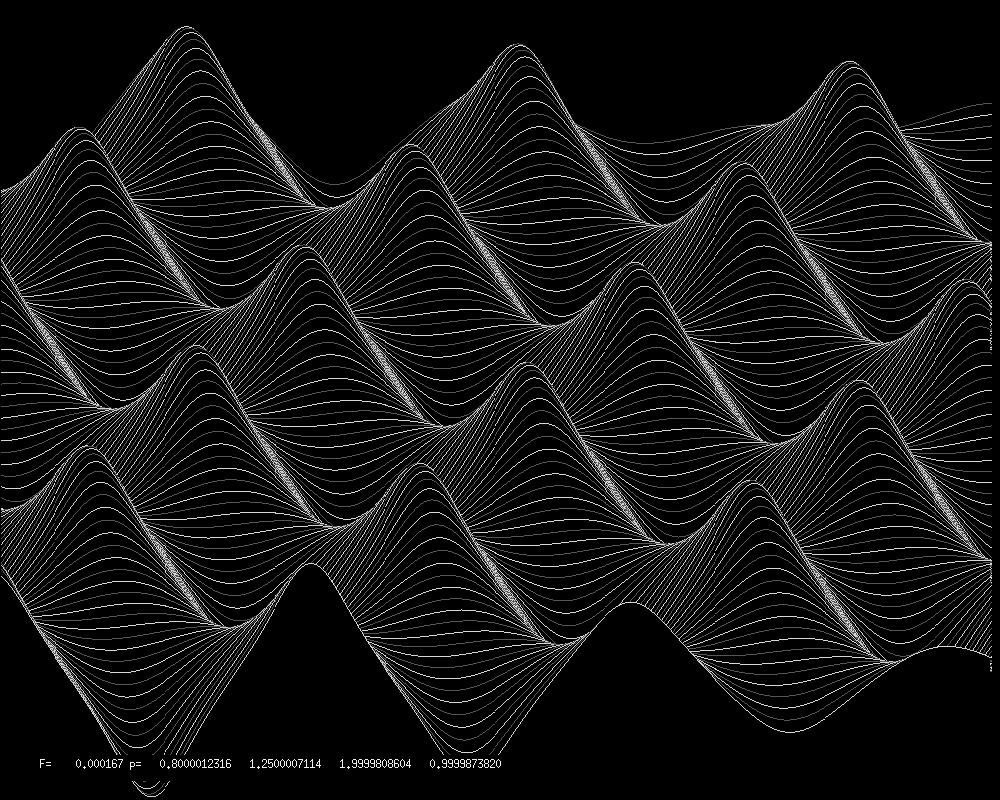
Höhenlinien:

Relief, halb durchsichtig:
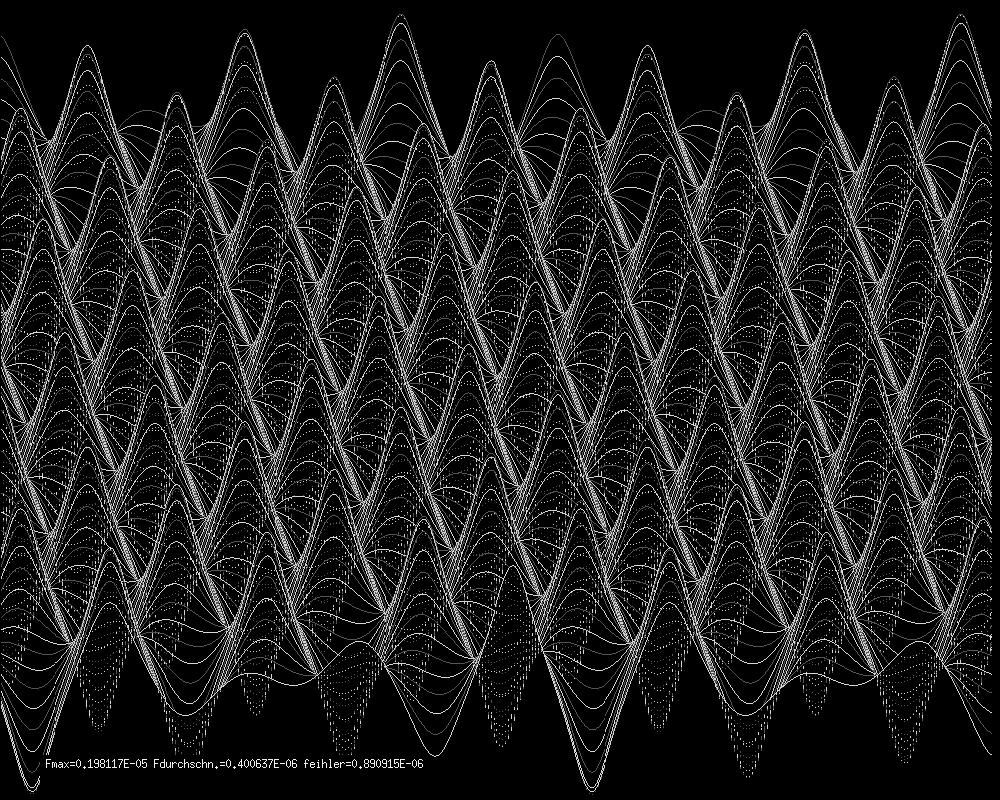
Relief, undurchsichtig:
Im dritten Teil betrachten wir die Interpolation eine Funktion durch ein
Polynom. Als Besonderheit sei dimarg=3 vorausgesetzt, d.h. bei Abbildungen von
Funktion und Polynom muss eine der Veränderlichen extra aber gleichartig
definiert sein.
Im gegebenen Zusammenhang wird deutlich - eine Beschreibung der zu lösenden
Aufgabe in ihren Einzelheiten zu einem geeigneten Zeitpunkt trägt nicht zum
Verständnis der gewünschten Lösung bei.
Vielmehr muss der Vorteil des durch direkte Kopplung an eine
im Betriebssystem enthaltene Programmentwicklungsumgebung wahrgenommen
werden.
Das gelingt z.B. durch Anwendung der Funktionen der Bourne-Shell, insbesondere
Editor vi, Compiler gfortran und Anwendung in der Programmiersprache
enthaltener Systemanweisungen. Es ist nicht ratsam, durch einen einzelnen
Programmaufruf einen gewünschten Endeffekt zu erzielen. Vielmehr werden alle
zur Orientierung gegebenen Anwendungsbeispiele durch ein strukturiertes
Shellprogramm bearbeitet. Dabei wechseln sich die Zeiten von Kompilierung,
Programmausführung, Datenein- und -ausgabe, Quelltexterzeugung gemäß einer zum
Zeitpunkt vorliegenden Datenmenge, und erneute Kompilierung usw. ab. Mehrere
der verwendeten Programmtexte werden automatisch von anderen Programmen in
Abhängigkeit von der Datenlage erzeugt, um später verwendet zu werden; im
gleichen betrachteten Anwendungsbeispiel. Z.B. "newtay.f" ist der
bisher längste und komplizierteste, automatisch von anderen Programmen erzeugte
Quelltext und Fortrankode. So können vergleichsweise kurze, einfache und stabil
anwendbare Programme entwickelt werden. Die Dateneingabe wird dabei ständig
kontrolliert. Durch die Eingabeprogramme selbst und genutzte Funktionen des
Betriebssystems. Insbesondere prüft der Compiler gfortran die Quelltexte und
beendet bei Fehlern den Ablauf des Anwendungsbeispiels. So ist notwendige
Korrektur sofort möglich und die Anwendung kann erneut gestartet werden. Und
zwar ab der Fehlerposition. Änderungen bereits akzeptierter Eingaben sind nicht
möglich. Das gilt vor allem auch für Einzeldaten. Derartige Änderungen
erfordern den Neubeginn der Anwendung.
Bei Betrachtung der Beispiele ist daher eine Unterscheidung der Aktivitäten im
Zusammenhang mit der wachsenden Dateneingabe zu beachten, um Beispiele
sinngemäß abzuwandeln. Und das zu ermöglichen, ist durch Vorlage eines
Quelltextes beabsichtigt.
Im bei Ausführung sämtlicher Beispiele nacheinander erzeugtem Protokoll werden
als Hilfestellung alle irgendwie vorgenommenen Eingaben durch die Textergänzung
' ! EINGABE ' markiert. Danach kann gesucht werden. Es
wird wenig eingegeben.
Hier folgen, ohne inhaltliche Einzelheiten zu nennen, die Bilder zur Interpolation
einer Funktion.
Höhenlinien der Funktion:

Höhenlinien der Interpolation:

Höhenlinien |funktion-Interpolation|:

Relief der Funktion, halb durchsichtig:
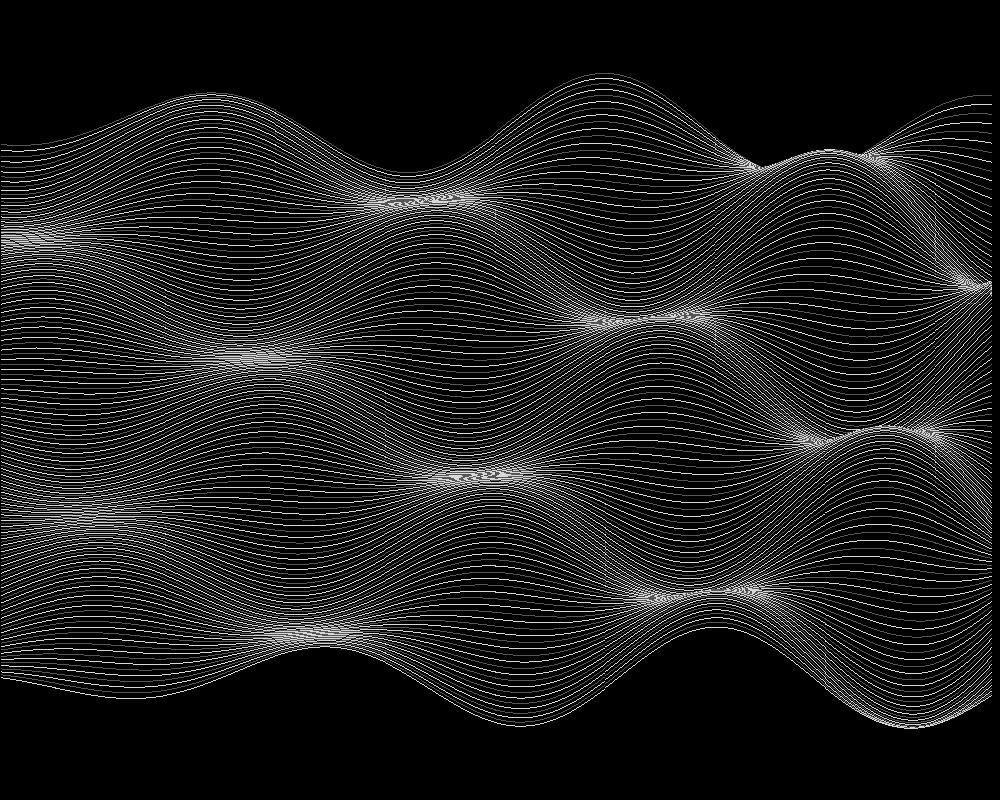
Relief der Interpolation, halb durchsichtig:
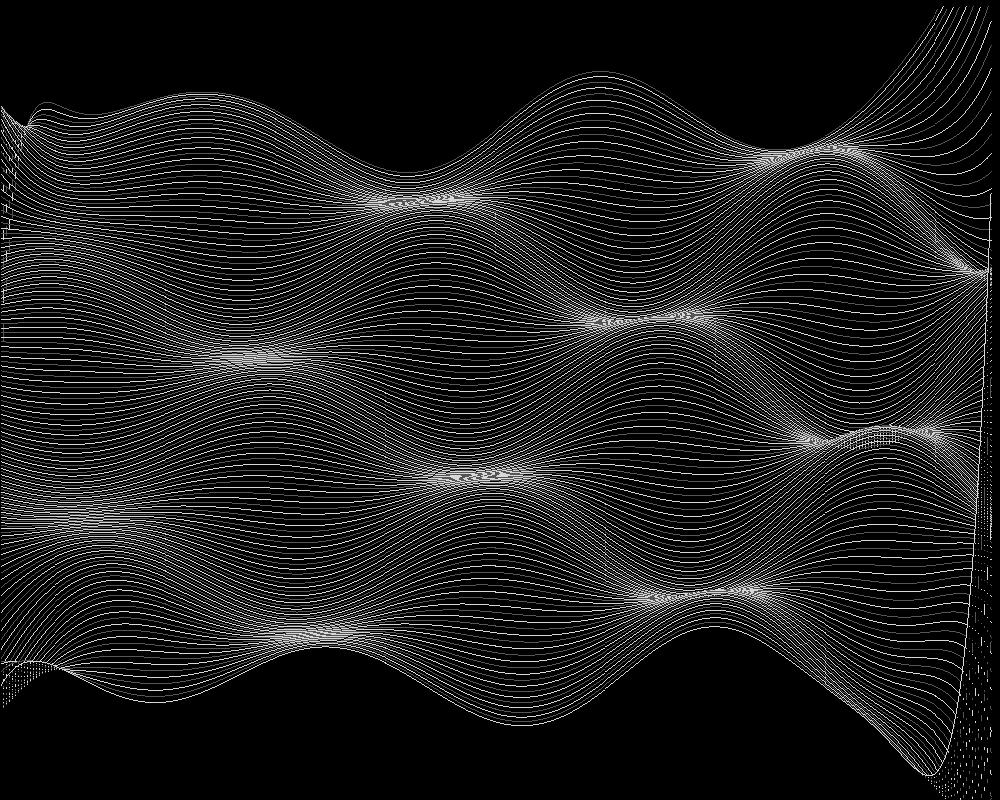
Im vierten Teil erfolgt die Approximation einer Funktion durch ein Polynom. Um
zu vergleichen, werden Funktion, Argument und die Darstellungsparameter
übereinstimmend gewählt:
(Grad)nung=20, dimarg=3, dimfn(20,3)=1771, ...
Worin unterscheiden sich Interpolation und Approximation?
Bei Interpolation werden Anzahl=dimfn Punkte im Definitionsbereich der Funktion
(hier ein Quader) zufällig gewählt nach dem Schema:
w=rand(), x(k)=xu(k)*w+(1-w)*xo(k), k=1,...,dimarg .
Allerdings wird der Punkt nur dann der Interpolationspunktmenge hinzugefügt,
wenn er zu allen bereits vorhandenen Punkten einen Mindestabstand mindist
einhält und die Anzahl dimfn noch nicht erreicht ist. Die Einordnung eines
Punktes wird bei Scheitern vielfach wiederholt, bevor mindist halbiert und der
gesamte Vorgang wiederholt wird. Auf jeden Fall wird am Ende eine
Interpolationspunktmenge mit mindist>0 und Anzahl = dimfn vorliegen. Nun
wird ein Gleichungssystem erzeugt mittels Anwendung von hornarg für alle
gegebenen Punkte. Bei jedem Punkt liefert die Funktion hornarg alle dimfn Werte
der Basispotenzen. Es gelten die Relationen:
Linearkombination der Basispotenzen (Punkt) = Funktionswert (Punkt) und so ein
Gleichungssystem vom Format [ dimfn x dimfn+1 ].
Mit Lösung des Gleichungssystems gewonnene Koeffizienten ergeben mit den dimfn
Werten von hornarg zu jedem Punkt des Definitionsbereiches der Funktion den
Wert des Interpolationspolynoms.
Bei Approximation werden (nz hier = 8000 >> dimfn
,Eingabewert) Punkte vorgegeben. Die Summe der Abweichungen von
(Linearkombination der Basispotenzen (Punkt) - Funktionswert (Punkt))^2 fällt
minimal aus, wenn die Ableitungen nach ihren Koeffizienten = 0
, so die "Methode der kleinsten Quadrate".
Die Bedingung trifft zu, wenn das (überbestimmt) Gleichungssystem vom Format [ nz x dimfn+1 ] mit seiner
transponierten Koeffizientenmatrix vom Format [ dimfn x nz ] multipliziert
wird:
In den folgenden Bildern zeigt sich der Vorteil einer Approximation:
Höhenlinien der Funktion:

Höhenlinien der Approximation:

Keine nennenswerte Differenz von Funktion und Approximation.
Relief der Funktion, halb durchsichtig:
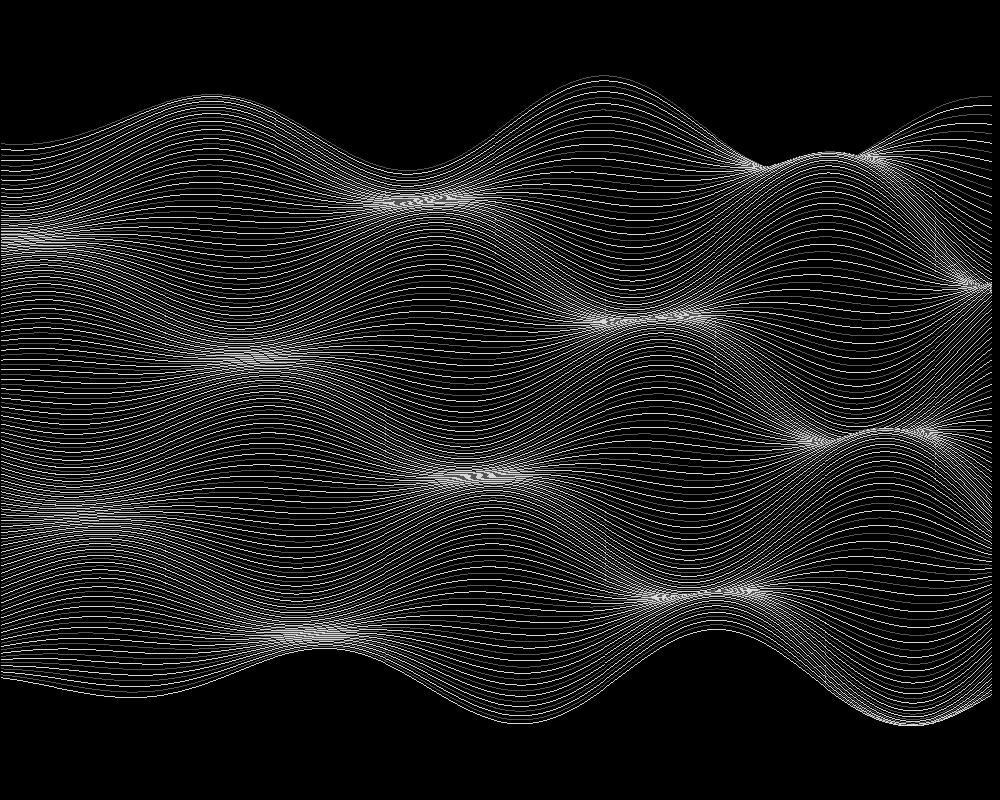
Relief der Approximation, halb durchsichtig:
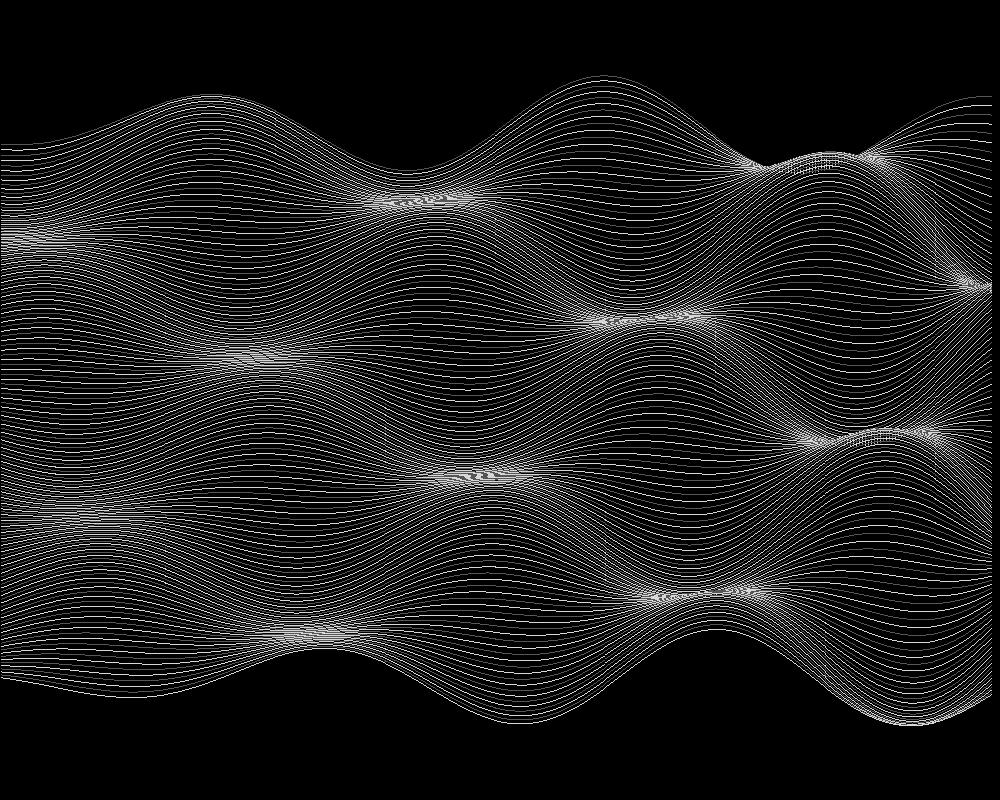
Im Teil 5 geht es wieder um die Approximation einer Punktmenge.
Bereits beim ersten Versuch im Teil 2 mussten neue Basisfunktionen sin(x(1)),
sin(x(2)) eingeführt werden, um eine brauchbare Approximation der gegebenen
Punktmenge zu bestimmen.
Oft sind weitere Verallgemeinerungen von Grundfunktionen erforderlich. Zur
Vereinfachung - der Fall dimarg=2. Dazu hier ein Beispiel:
Grundfunktionen g1(x1)=sin(p(1)*x1+p(3)), g2(x2)=sin(p(2)*x2+p(4)), sind
variabel in zusätzlich 4 Parametern.
Und die gesuchte minimale Abweichung der Approximation von der gegebenen
Punktmenge erfolgt durch Berechnung geeigneter Werte p(1),...,p(4)
.
Die Berechnung erfolgt durch ein experimentelles dimp-dimensionales Newtonverfahren. Dabei
werden Differentialquotienten durch entsprechende Differenzenquotienten
ersetzt. Im Zusammenwirken mit der Funktion param.f erfolgt im automatisch
erzeugten Programm newtay.f die Bereitstellung der hier benötigten 33
Punktabweichungen und anschließend die Bestimmung der Quotienten. Dann kann das
(hier) [ 4 x 5 ] - Newtonsystem
[delta(p)=delta2(p)*diff(p)] nach diff(p) gelöst werden, um die jeweils nächste
Iteration auszuführen.
Dabei kann und muss die Differenzschrittweite systematisch variiert werden mit
dem Ziel, so eine Mindestkonvergenzrate von 5% zu erzielen. Wenn das nicht mehr
erreicht werden kann, ist die Berechnung abgeschlossen.
Weiterführende Erkenntnisse entnimmt man dem Quellkode der Programme und Shellprozeduren.
Um das zu erleichtern existiert hier die Prozedur search.
Z.B. zeigt ./search . '*' 'EINGABE' alle
Quelltextstellen, wo EINGABE vorkommt. Interessant wäre z.B. auch 'system',
usw.
Nun folgen die Bilder des letzten Teiles.
Darstellungen der Punktmenge:
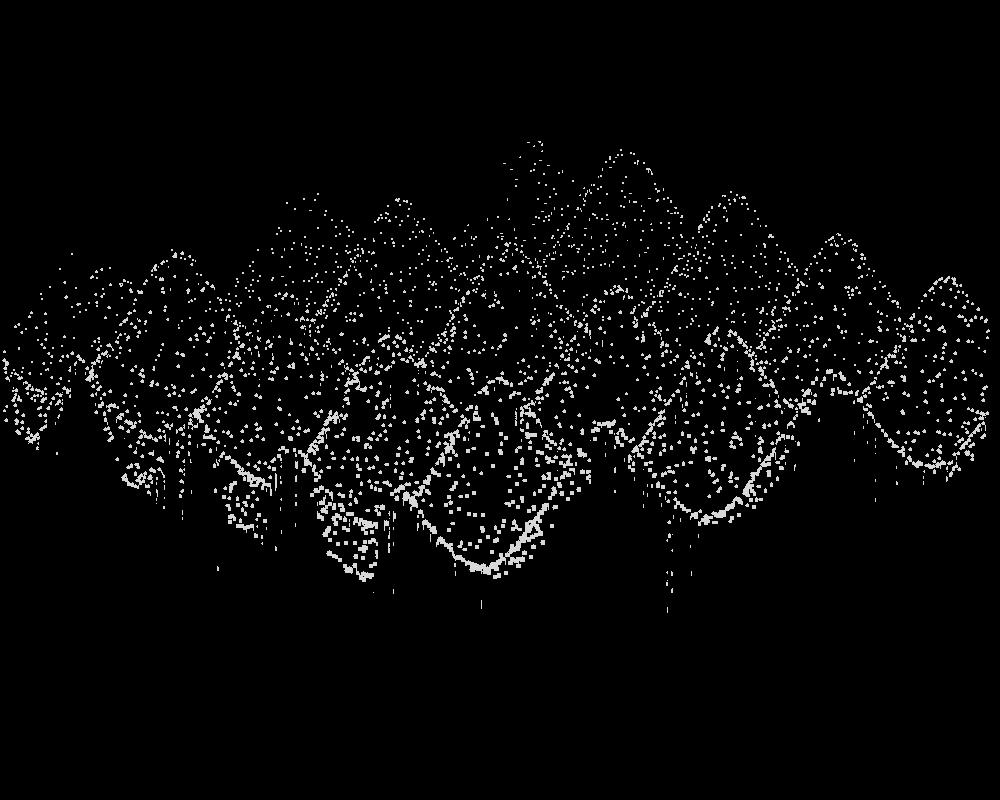
Höhenlinien:

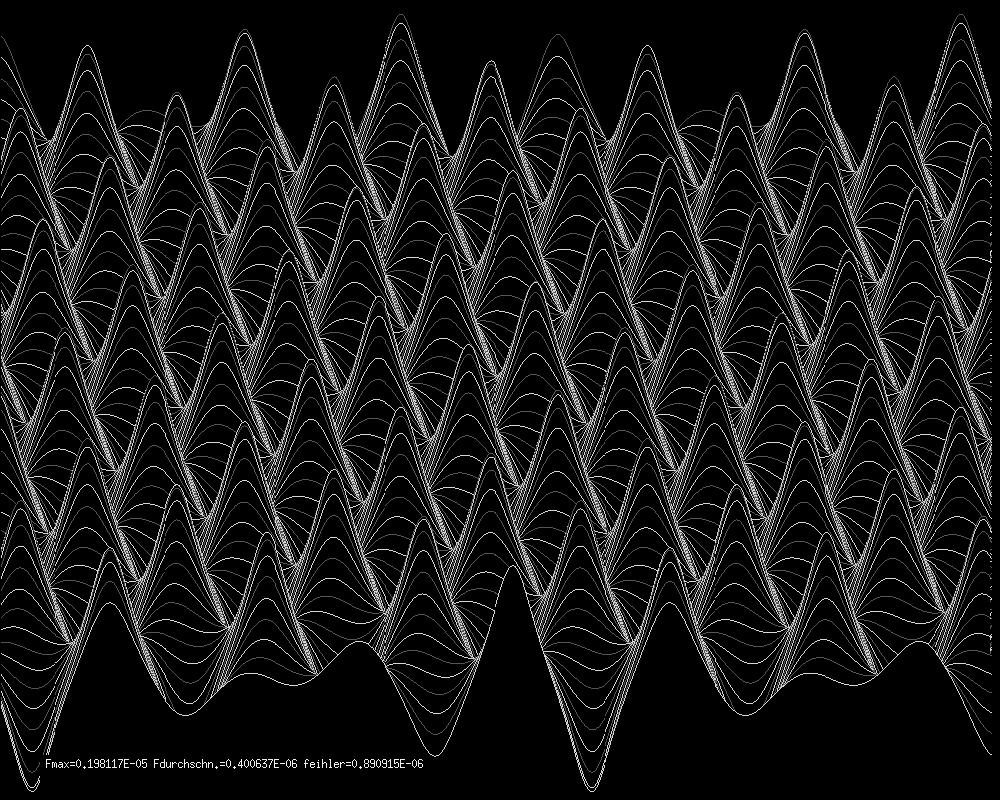
Relief, halb durchsichtig:
Relief, undurchsichtig: