Kompositionsgruppe

Im Folgenden wird betrachtet:

Funktionen f(x) und g(x) werden verknüpft durch Substitution f o g := f(g(x). So entsteht eine Halbgruppe.

Hier gegebene Voraussetzungen für zu verknüpfende Funktionen f(x) :

1. Taylorentwicklung um den Punkt x=0, Taylor(f(x),x,n,0), für jede Integer-Zahl n existiert

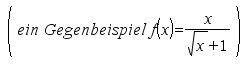
2. f(0)=0 und (für die Ableitung) f’(0) <> 0.

Dann ergibt sich eine Gruppe von Funktionen f(x).

Im Allgemeinen führt bereits die Multiplikation f o g zu unbekannten Funktionen. Daher werden in den vorliegenden Programmen an Stelle der Funktionen die entsprechenden Taylorentwicklungen, Taylor(f(x),x,n,0), betrachtet. Die Größe n muss passend zum betrachteten Zusammenhang gewählt und abgespeichert werden, z.B. n:=7, mittels initnnull(7).

Achtung: Mit n vergrößert sich die Rechenzeit am Taschencomputer extrem.

Ob eine gewählte Anwendung tatsächlich zu einem Intervall (u<=x<=o, u<0, o>0) führt, in dem die Potenzreihe = Taylor(f(x),x,n,0) mit n -> <unendlich> konvergiert, wird mit den hier gegebenen Programmen nicht untersucht.

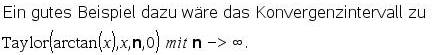
Die hier betrachteten Funktionen bilden also eine Gruppe. Daher können mehrere Programme angewandt werden:

Invertieren f^(-1), Potenzieren f^p (p Integer, Assoziativgesetz ermöglicht das Potenzieren),

Wurzel f^(1/2), d.h. g(x)=f^(1/2)(x) ist diejenige Funktion, für die gilt g(g(x))=f(x) und

unter Verwendung von Invertieren, Wurzel und Potenzieren mit Integer-Exponenten ist auch Potenzieren mit rationalen Exponenten möglich.

In der folgenden Abbildung ein Beispiel:

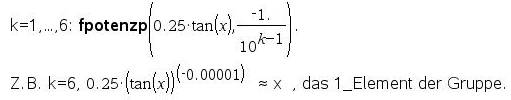
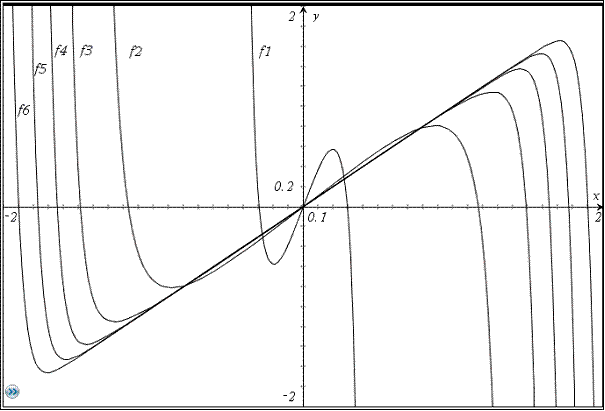
Hier das entsprechende Programm für den Taschencomputer TI-Nspire

Vor Anwendung der gegebenen Programme muss initialisiert werden:

Dabei werden die Größen n und null definiert, um das Ergebnis der Taylorentwicklung einer Funktion zu beeinflussen. Die Ordnung wird durch n bestimmt und der Entwicklungspunkt durch null. Bei null =0 erfolgt eine exakte Berechnung der Koeffizienten, bei null =0. eine approximative Berechnung mit Gleitkommazahlen, Genauigkeit 10^(-12).

Auf dem Taschencomputer ist die Ordnung n > 2 und < 29 zu wählen. Dabei muss evtl. je nach Berechnungsbeispiel die Ordnung reduziert werden, um zu einem Resultat zu gelangen.

Bei einer Berechnung sollte die Ordnung von kleinen Werten in mehreren Schritten gesteigert werden, um die Rechenzeit einschätzen zu können. So werden auch Zwischenergebnisse gewonnen, bevor eine Berechnung bei zu großer Ordnung evtl. scheitert.

Und weiter:

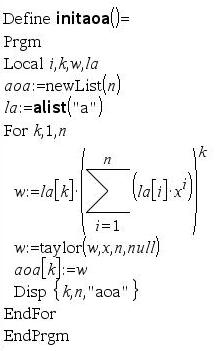
Hier noch einige Hilfsprogramme:

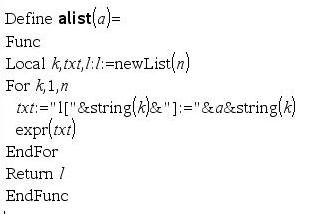
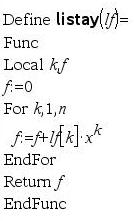
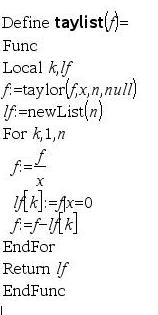
Es folgen einige nützliche Programme:

In einer nicht abelschen Gruppe ist der Kommutator f o g o f^(-1) o g^(-1) interessant:

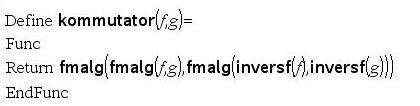
Prüft, ob f(x) ein Gruppenelement ist:

Potenz f^p mit rationalem Exponenten p, wobei (0<=|p|<1024)

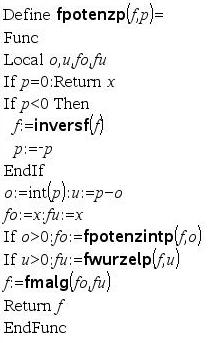
Inverse einer Funktion f(x)

Berechnet Wurzel f^(1/2)

Berechnet Wurzel f^(1/p)

Berechnet f^p mit rationalem p wobei 0<=p<1, Genauigkeit von p 2^(-30)<0.000000001

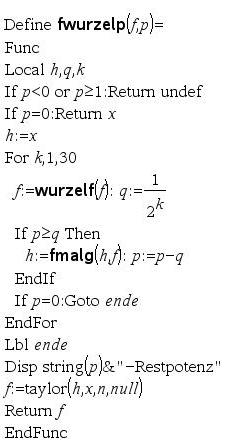
Berechnet f^p mit integer p<=1023

f o g ,d.h. f(g(x))

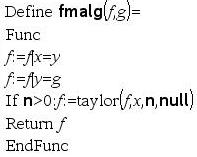
Berechnungsbeispiele

Hier weitere Funktionen:

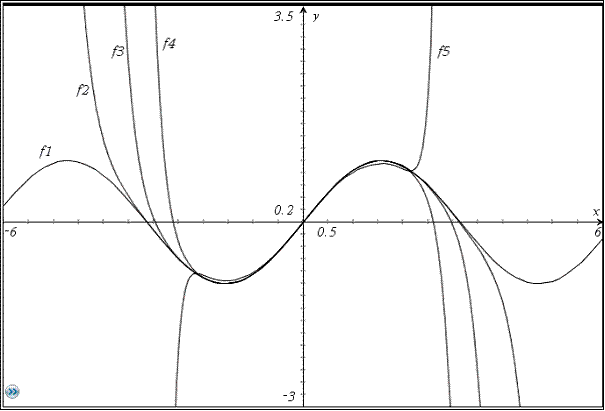
Bildwiedergabe mit Hilfe des ProgrammsHH inversf

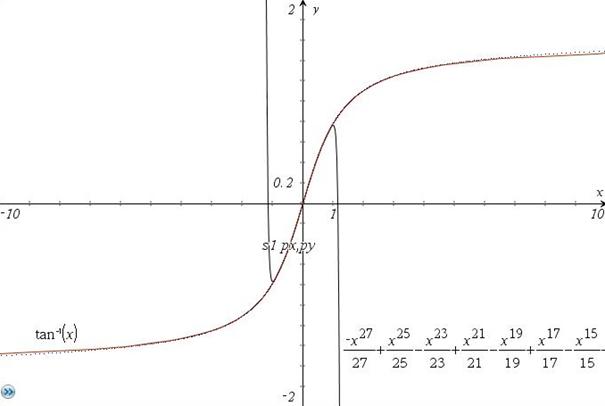
Bei Anwendung der zuvor beschriebenen Programme werden Taylorpolynome erzeugt. Oft ist es sogar möglich, mit Induktion die weiteren Koeffizienten einer Potenzreihe zu bestimmen, die als Fortführung des gegebenen Polynoms anzusehen ist. Das ist erfreulich. Um die gewonnene Funktion einzuschätzen, ist jedoch eine Bildwiedergabe der Funktion wünschenswert. Auf Grund der Koeffizienten kann ein Konvergenzbereich für das Argument erkannt werden. Dieser Bereich wird auch schon bei Anwendung des Taylorpolynoms deutlich. Nur innerhalb der erkannten Grenzen ist eine grafische Darstellung des Polynoms anschaulich. Ein Beispiel dafür, das polynom := taylor (arctan(x),x,n,null) Konvergenzintervall (-1 < x <1 ). Mit wachsender Ordnung n wird in diesem Intervall die Darstellung genauer, außerhalb nützt n nichts. Wenn also ein Polynom berechnet wurde und das zu erwartende Konvergenzintervall klein ausfällt, hat die Mühe der Berechnung keinen Lohn, außer man kann inversf erfolgreich anwenden. Das so erzeugte Polynom muss bei der Bildwiedergabe allerdings mit vertauschten Rollen für Argument und Funktionswert (y,x) dargestellt werden. Dabei gewinnt man in vielen Beispielen eine großzügige Übersicht, ein großes Darstellungsintervall.

Hier folgt das Programm bildinvers

Aufruf des Programms mit Polynom der Ordnung 25 :

Bilddarstellung von Polynom und invertiertem Polynom mit Tausch Argument und Funktion :

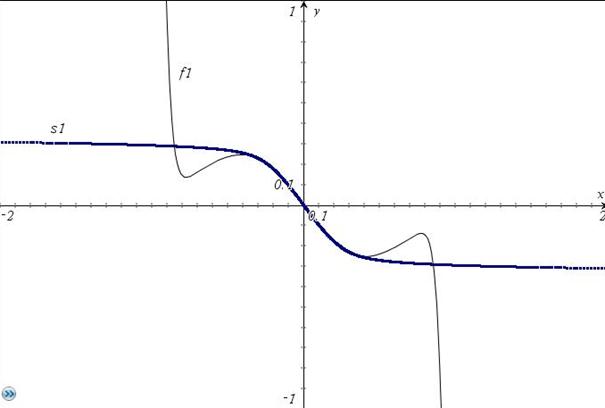
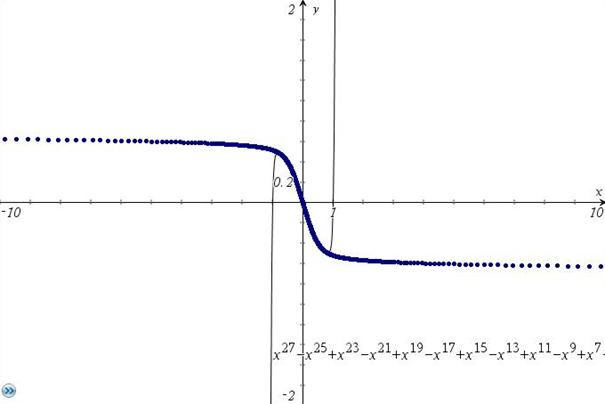
Übersichtdarstellung, allerdings mit Ordnung 27 (im Intervall (-1,1) Polynom genauer) :

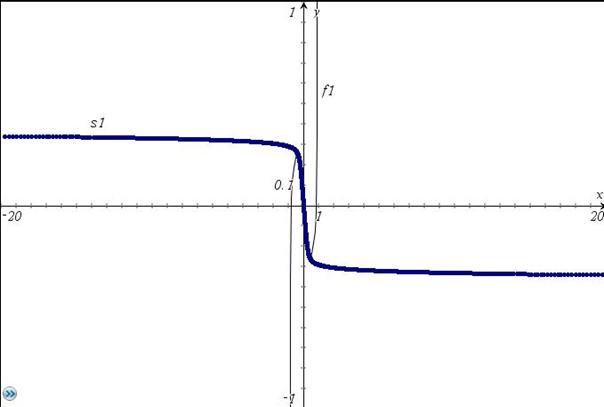
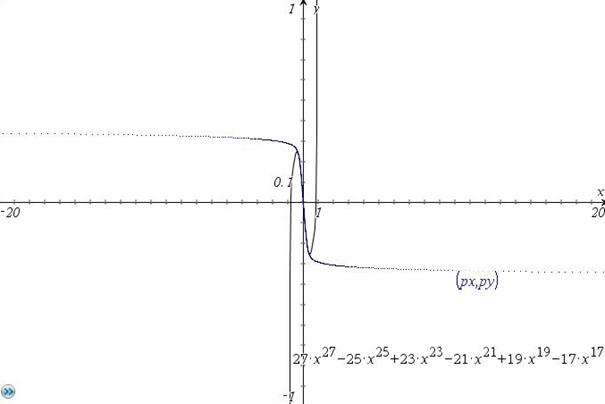
Auch bei größerem Konvergenzintervall kann bildinvers vorteilhaft sein. Es werden im günstigen Fall auch Zweige der Funktion angezeigt (arcsin(x)) :

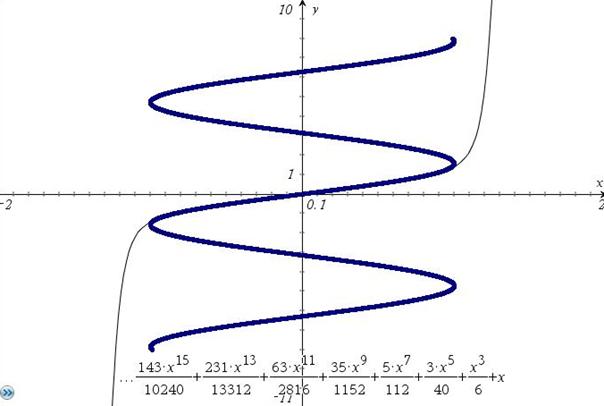
Weitere Beispiele:

Die genaue Berechnung einer Wurzel f^(1/p), Integer p, erfordert zusätzliche Rechenzeit. Z.B.