Gravitationsfunktion

Voraussetzungen:
1. ballistische Lichtausbreitung
2. Abdrift der logarithmisch Normalverteilten Frequenzen des Lichtes
3. statisches Universum

Betrachtet werden zwei Simulationen und resultierende Bedingungen
1. Rotation einer Galaxie
Simulationszeitraum: 10^9 Jahre
Vereinfachungen Startwerte für
Anzahl der Masseansammlungen mk = 5550 mit durchschnittlicher Größe von 4*10^37_kg ,
Positionen in einem Rotationsellipsoid, Größe wie Milchstraße, zum Zentrum zunehmend dichter und
Anfangsgeschwindigkeiten entsprechend Position zum Zentrum.
Bedingung: Simulation erfolgreich, wenn Galaxie nicht "explodiert" und nicht "implodiert", d.h. alle Masseansammlungen beteiligen sich während des Simulationszeitraums in "engem Umlauf" an der Rotation. Dabei ergibt sich für die durchschnittliche Geschwindigkeit V = Summe vk * mk / Summe mk , die maximale Geschwindigkeit MAXV = max vk und die kinetische Energie E = Summe 1/2 * mk * vk^2 ein typischer Verlauf:

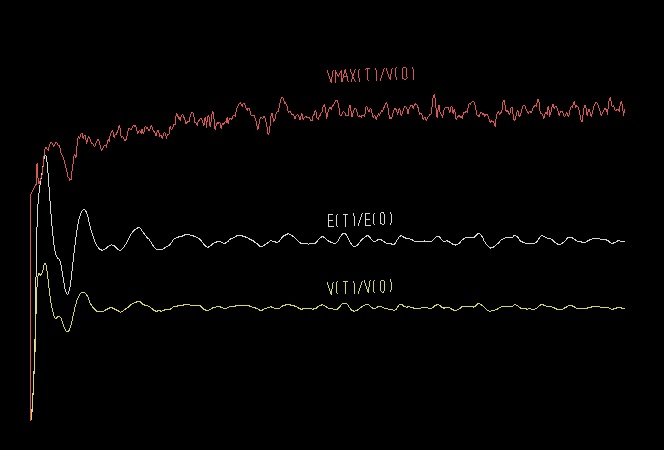
2. Positionierung von Galaxien
Simulationszeitraum 10^10 Jahre
Vereinfachungen Startwerte für
Anzahl der Galaxien mk = 5550 mit "durchschnittlicher" Größe von 2*10^41_kg ,
Positionen Gleichverteilt in einem Würfel, so dass die durchschnittliche Dicht des Universums resultiert, und
Anfangsgeschwindigkeiten im Intervall [0,0.001_c], Gleichverteilt, Richtung (rundum) Gleichverteilt.
Bedingung: Simulation erfolgreich, wenn am Ende des Simulationszeitraums die Galaxien "fraktal positioniert" sind.
Typischer Verlauf von Maximalgeschwindigkeit, durchschnittlicher Geschwindigkeit und kinetischer Energie:


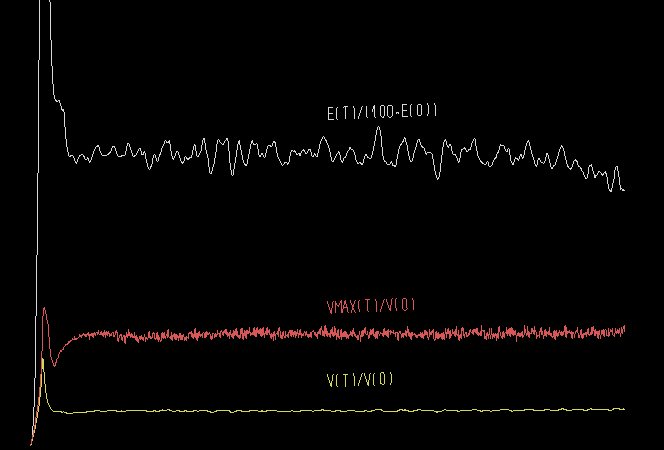
Das 1. Beispiel ist nur dann erfolgreich, wenn ein logarithmisches Potential als Komponente LG in der Gravitation berücksichtigt wird.
Zur Veranschaulichung wird der Übergangspunkt LG=G betrachtet oder, umgekehrt, vorgegeben. Er kann auch grob geschätzt werden, z.B. 3000_ltyr, und Beispiel 1 ist immer noch erfolgreich.
Das 2. Beispiel ist nur dann im Sinne der Beschreibung erfolgreich, wenn zusätzlich ein lineares Potential als eine weitere Komponente -G0 in der Gravitation auftritt. Auch hier ist ein Übergangspunkt LG-G0=0 in Abhängigkeit der durchschnittlichen Dichte grob zu schätzen, z.B. 5*10^7_ltyr, und Beispiel 2 ist erfolgreich.
Beide Beispiele blieben allerdings auch bei einer etwas anderen Wahl der Übergangspunkte erfolgreich.
Die Intervalle, in denen die jeweiligen Übergangspunkte liegen, sind nicht bekannt. Eine Bestimmung der Intervallgrenzen dürfte sehr aufwendig sein.
Die genaue Kenntnis der Potentiale und ihrer zugeordneten Übergangspunkte ist wünschenswert. Man kann sie durch die Vorgabe einer Gravitationsfunktion gf(r) gewinnen, sofern gf(r) zutrifft. Hier z.B. folgende Definition:






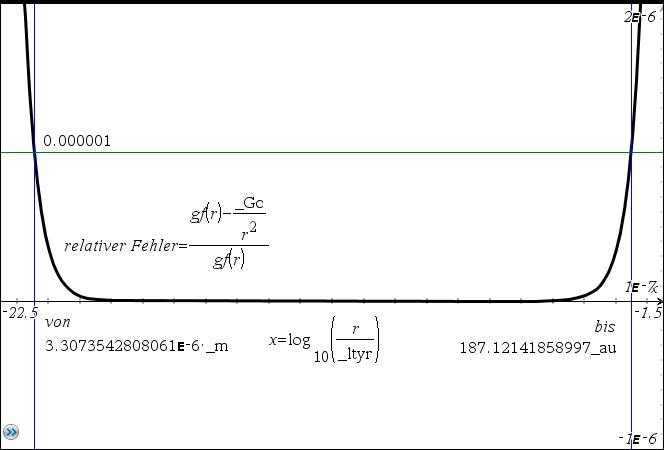
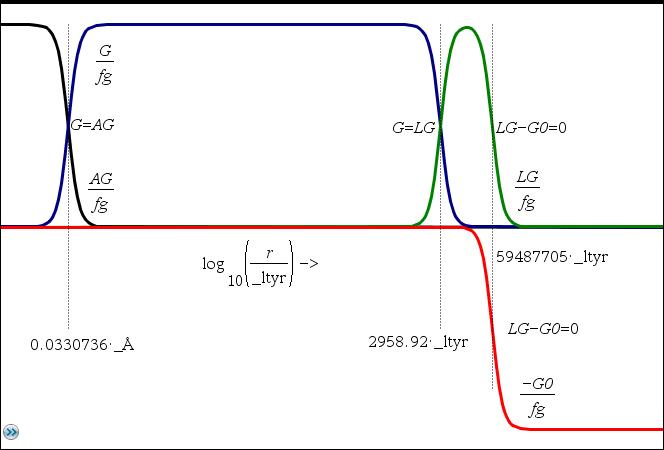
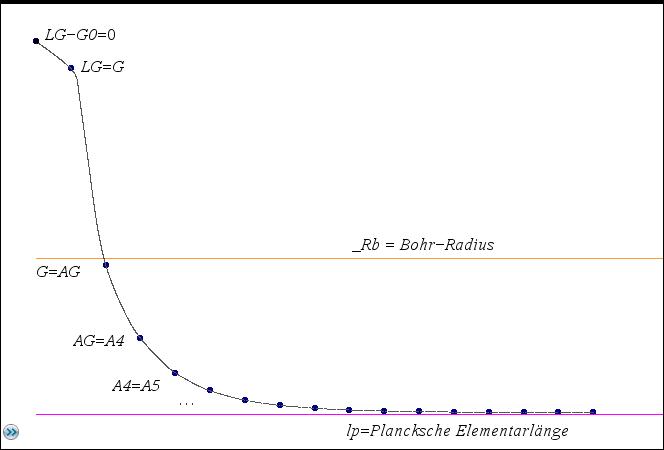
bzw. =

Mittels Gravitationsfunktion gf(r) kann wie bei der Gravitation _Gc/r^2 die Anziehungskraft zwischen zwei
Massen m1 , m2 an den beiden Positionen [x1,y1,z1] , [x2,y2,z2] berechnet werden,
Hilfsgrößen r = sqrt((x1-x2)^2+(y1-y2)^2+(z1-z2)^2) und xyz21 = [x2-x1,y2-y1,z2-z1],
vorausgesetzt, die Ausdehnung der Massen ist klein gegenüber ihrem Abstand r:

gf12 = xyz21 * m1 * m2 * gf(r) / r    bzw.   g12 = xyz21 * m1 *m2 * _Gc / r^3
und der Kraftvektor wirkt in beide Richtungen gf12 = -gf21 bzw. g12 = - g21.

Sind die Kräfte zum aktuellen Zeitpunkt bekannt, können die aktuellen Beschleunigungen berechnet werden (Kraft/Masse=Beschleunigung):

bfm12 = xyz21 * m2 * gf(r) / r    bzw.   bm12 = xyz21 * m2 * _Gc / r^3 und
bfm21 = -xyz21 * m1 * gf(r) / r    bzw.   bm21 = -xyz21 * m1 * _Gc / r^3.

Die Vektoren bfm12 bzw. bm12 beschleunigen die Masse m1. Sind in einem System mehr als zwei Massen vorhanden, sind die entsprechenden Beschleunigungsvektoren, die noch einen nennenswerten Beitrag zur Gesamtbeschleunigung erbringen, für eine betrachtete Masse zu addieren, um den resultierenden Beschleunigungsvektor für diese Masse zu bestimmen. Sind diese Vektoren für alle Massen bestimmt, kann die Bewegung der Massen numerisch simuliert werden, vorausgesetzt Startwerte für Anfangspositionen und Geschwindigkeitsvektoren sind gegeben.

Zur Veranschaulichung der Unterschiede der Beschleunigungsvektoren, die bei Anwendung von gf(r) bzw. _Gc/r^2 resultieren, folgen hier
vier Berechnungsbeispiele:
1. Beschleunigung des Planeten Jupiter durch die Sonne:
Sonne , Masse=1.99*10^30_kg , Position =[0,0,0]
Jupiter , Masse=1.9*10^27*_kg , Position =[5.2026_au,0,0]
Beschleunigung Jupiter = [-0.000219*(_m/(_s^2)),0,0] bzw. = [-0.000219*(_m/(_s^2)),0,0]
Beschleunigung Sonne = [2.0934410^(-7)*(_m/(_s^2)),0,0] bzw. = [2.0934410^(-7)*(_m/(_s^2)),0,0]
2. Beschleunigungen bei Sonne und "Nemesis"
Sonne , Masse=1.99*10^30_kg , Position =[0,0,0]
"Nemesis" , Masse = 8.4*10^28_kg , Position =[50134_au,0,0]
Beschleunigung "Nemesis" = [-2.36185*10^(-12)*(_m/(_s^2)),0,0] bzw. = [-2.36122*10^(-12)*(_m/(_s^2)),0,0]
Beschleunigung Sonne = [9.96963*10^(-14)*(_m/(_s^2)),0,0] bzw. = [9.96696*10^(-14)*(_m/(_s^2)),0,0]
3. Beschleunigungen bei Sonne und Sirius B
Sonne , Masse=1.99*10^30_kg , Position =[0,0,0]
Sirius B , Masse=1.95*10^30*_kg Position =[8.6_ltyr,0,0]
Beschleunigung Sirius B = [-2.01226*10^(-14)*(_m/(_s^2)),0,0] bzw. = [-2.00643*10^(-14)*(_m/(_s^2)),0,0]
Beschleunigung Sonne = [1.97182*10^(-14)*(_m/(_s^2)),0,0] bzw. = [1.9661*10^(-14)*(_m/(_s^2)),0,0]
4. Beschleunigung bei Galaxie 1 und Galaxie 2
Galaxie 1 , Masse =2*10^41_kg , Position =[0,0,0]
Galaxie 2 , Masse =5*10^41_kg , Position =[5*10^7,-2*10^7,-3*10^7]_ltyr
Beschleunigung Galaxie 2 = [2.40096*10^(-14),-9.60385*10^(-15),-1.44058*10^(-14)]*(_m/(_s^2))
bzw. = [-3.18341*10^(-17),1.27337*10^(-17),1.91005*10^(-17)]*(_m/(_s^2))
Beschleunigung Galaxie 1 = [-6.00241*10^(-14),2.40096*10^(-14),3.60144*10^(-14)]*(_m/(_s^2))
bzw. = [7.95853*10^(-17),-3.18341*10^(-17),-4.77512*10^(-17)]*(_m/(_s^2))
Im 4. Beispiel Vorzeichenumkehr des Beschleunigungsvektors bei Anwendung von gf(r) beachten.

Linux-Programme zur Rotation einer Galaxie bzw. zur Positionierung von Galaxien

Bedingung - Haftungsausschluss ausnahmslos für alle kostenfrei übernommenen Leistungen.

Rechentechnische Vorgaben:
Die hier vorliegenden Programme wurden unter dem Betriebssystem SUSE Linux 12.1 entwickelt und setzen voraus
X-Windows, gcc und gfortran
Mittels Anpassung könnten die vorliegenden Programme evtl. auch unter leicht modifizierten Voraussetzungen funktionieren.

Voraussetzungen:
Bereits erwähnt - ballistische Lichtausbreitung, statisches Universum, Abdrift der logarithmisch Normalverteiten Frequenzen des Lichtes.
Ein statisches Universum muss in Zeit und Raum unbegrenzt sein. Andernfalls führt die Komponente -G0 der Gravitationsfunktion gf unweigerlich zu seiner Ausdehnung, d.h. es wäre nicht statisch. Das erfordert eine weitere Voraussetzung - das Universum muss in bestimmter Weise "homogen" sein.
Betrachten wir dazu:
Um eine beliebige Position P eine Kugelschale SPab = Menge aller Punkte Q mit a < | P - Q | < b, wobei b >> a,
und einen Kegel KPvε = Menge aller Punkte Q in einem Kegel mit der Spitze P in Richtung eines Vektors v mit einem kleinen Öffnungswinkel ε > 0.
Der Wert gPabvε+ = Summe über alle Massen m(Q) im Durchschnitt von SPab und KPvε der Funktion m(Q)*gf(|Q-P|) unterscheidet sich von
gPabvε- in der entgegengesetzten Richtung um die Größe wPabvε+- und
mit b -> unendlich strebt wPabvε+- gegen eine endliche Größe wPavε+-.
Ferner ist der Grenzwert a -> unendlich für wPavε+- = 0 .Das gelte für jeden beliebig gegebenen Punkt P, jeden Einheitsvektor v und jeden kleinen Winkel ε > 0.

Vereinfachungen in der Sache:
An Stelle von einzelnen Massepunkten werden Masseansammlungen mk mit endlicher Ausdehnung rmk betrachtet. Falls der Abstand rki zweier Masseansammlungen mk und mi groß ist gegenüber ihren Ausdehnungen rmk bzw. rmi, kann die Gravitationsfunktion gf ohne allzu große Fehler angewandt werden. Falls das nicht zutrifft, z.B. wenn rki = 0, sind die interne Verformung einer beteiligten Masseansammlung durch Gravitation und evtl. Kollisionen einzelner Teilnehmer (Umwandlung von Bewegungsenergie in Wärmeenergie) als eine Dezimierung der potentiellen Energie zu berücksichtigen. Hier wird folgende Vereinfachung festgelegt:
rkiwirksam = sqrt ( rki^2 + rmk^2 + rmi^2 )    und es wird grundsätzlich mit dem wirksamen Abstand gf(rkiwirksam) gerechnet.
Ausnahme: Großflächige Verteilung von Masseansammlungen mit dem Durchmesser a, dann wird bei der Bestimmung einer Kreisgeschwindigkeit mit r + a gerechnet.
Bei der Positionierung von Galaxien wird nur der Inhalt eines geeignet dimensionierten Würfels betrachtet. Die Umgebung wird mit ihren gegebenen gravitativen Auswirkungen nicht berücksichtigt. Daraus resultiert die Tendenz, dass Galaxien der Simulation den Würfel verlassen. Sie werden "hinausgezogen" oder wegen der Komponente -G0 auch "herausgedrängt". Hier erfolgt nun folgende Vereinfachung:
Wie Galaxien den Simulationswürfel verlassen, so gelangen Galaxien aus den gedachten Nachbarbereichen auch in den Würfel zurück. Dabei ist ein Ausgleich bezogen auf die gesamte Masse aller verlorenen und gewonnenen Galaxien und ihrer kinetischen Energie über einen Zeitraum gegeben. Es wäre schwer, dies mittels Zufallzahlengenerators zu programmieren. Daher wurde im vorliegenden Programm posgal für jede den Würfel verlassende Galaxie eine in den Würfel eindringende mit der gleichen Masse angenommen. Dabei bleibt der Geschwindigkeitsvektor konstant aber die Position wechselt die Seiten:
Bei Austritt an eine Ecke oder Kante des Würfels wird die Position am Mittelpunkt des Würfels gespiegelt, bei Austritt über eine Begrenzungsfläche, der häufigere Fall, erfolgt der Eintritt an der gegenüberliegenden Begrenzungsfläche, jedoch dort mit zufälliger Position. Auf diese Weise soll ein systematischer Fehler des geschilderten Vorgehens verringert werden.
Es ist dahingestellt, ob derartige Vereinfachungen noch zu qualitativ zutreffenden Ergebnissen führen.