Bei Interesse kann hier das verwendete Programm samt Beispielen für HP48GX kostenlos heruntergeladen werden (rechte Maustaste), vorausgesetzt, man akzeptiert, daß keinerlei Haftung für irgendwelche Schäden übernommen wird, die im Zusammenhang mit dem Herunterladen, dem verwendeten Programm oder den Beispielen oder den Ergebnissen des Programms stehen könnten.

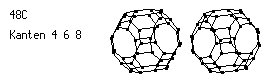
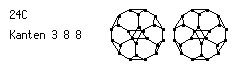
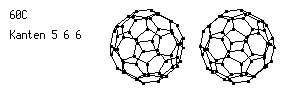
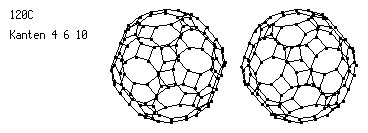
Raumfüllende Strukturen entstehen, wenn jedes Kohlenstoffatom mit vier weiteren eine Verbindung eingeht. Dabei soll die Bedingung der Kongruenz zweier beliebiger Eckpunkte (Atome einschließlich Bindungen) der Struktur beibehalten werden.

Um ein Haar, um die kleine Winkelabweichung von 1,5 Grad, hätte das Dodekaeder (Kanten:5,5,5) als Grundfigur einer Kristallstruktur dienen können. Wir betrachten statt dessen zwei bekannte Strukturen:

1. Diamant - alle Bindungen in jedem Eckpunkt erfolgen kugelsymmetrisch, d.h. je zwei beliebige Bindungen schließen ein und denselben Winkel ein.

2. Graphit - in Schichten bilden sich sechseckige Bindungsringe aus, je zwei benachbarte Schichten sind über verlängerte Bindungen jeder zweiten Ecke verknüpft.

Eine Übersicht entsteht bei der Darstellung einer Kugel mit einem Durchmesser von 7 Bindungslängen, Diamant: 123C, Graphit: 105C, unter Beachtung der Sichtbarkeitsverhältnisse (Vermeidung verdeckter Kanten). Man muß nur geduldig das mittlere Bild betrachten, bis alle störenden Einflüsse entfallen und wird dann durch eine glasklare Darstellung belohnt.

         



           Funktionalgleichungen numerisch mit dem Taschenrechner HP48GX lösen
Orientieren wir uns am Beispiel der Winkelfunktionen sin(x) und cos(x). Sie genügen bekanntlich den Additionstheoremen, allgemein formuliert (f, g an stelle von sin ,cos):
            f(x+y)=f(x)*g(y)+f(y)*g(x) , g(x+y)=g(x)*g(y)-f(x)*f(y).
Es ergibt sich die Frage, ob die Winkelfunktionen als einzige die Additionstheoreme befriedigen. Wir setzen über evtl. Lösungsfunktionen voraus, sie seien stetig. Man kann diese Voraussetzung noch abschwächen, aber wir wollen keine Haarspalterei betreiben. Mit dem HP48GX ist eine numerische Behandlung der genannten Frage möglich. Ähnlich der numerischen Lösung von Randwertaufgaben bei gewöhnlichen Differentialgleichungen werden hier stetige Lösungen von Funktionalgleichungen einfachen Typs numerisch bestimmt. Allerdings kann im Unterschied zu Differentialgleichungen das Darstellungsintervall der Lösung nicht willkürlich vorgegeben werden, sondern der Intervallanfang ist durch den Typ der Funktionalgleichung bestimmt. Es werden zwei Möglichkeiten vorgesehen. Und zwar:
            Beginnt die Gleichung mit f(x+y)=G, dann beginnt das Intervall mit 0, oder die Gleichung beginnt mit f(x*y)=G, dann beginnt das Intervall mit 1; f  bezeichnet dabei die gesuchte Funktion bzw. den gesuchten Funktionenvektor, falls es ein System ist. Dabei muß die Funktionalgleichung invariant sein gegenüber arithmetischen Gesetzen im Argument:
            Kommutativgesetz, d.h. Symmetrie der Fgl. f(x o y) = G(f(x),f(y)) = G(f(y),f(x)) und
            Assoziativgesetz    f(x o y o z) = G(G(f(x),f(y)),f(z)) = G(f(x),G(f(y),f(z))) , o={+,*} .
Als Intervalle können nur auftreten: 0<=x oder x<=0 für das Argument (x+y) bzw. 1<=x oder 0<x<=1 für das Argument (x*y).  Und jeder Vorgabewert für die Funktion muß im jeweiligen Intervall liegen; im gegebenen HP48-Programm wird sogar seine Lage oberhalb des Startwertes ( 0 oder 1 ) vorausgesetzt. Trotz dieser Einschränkung erlaubt eine numerische Bestimmung von stetigen Lösungen einen guten Einblick in die Vielfalt der möglichen Lösungen der Funktionalgleichung. Eine weitere Einschränkung ergibt sich hier für den Typ der zulässigen Funktionalgleichungen. Sie resultiert daraus, daß für den Anfangspunkt des Intervalls die Bedingung der Auflösbarkeit erfüllt ist, d.h. f(x)=G(f(x),f(0)) läßt sich eindeutig nach f(0) bzw.  f(x)=G(f(x),f(1)) nach f(1) auflösen und das Resultat ist unabhängig von x. Alle diese Bedingungen können im vorliegenden HP48-Programm nur im Nachhinein durch Einsetzen der berechneten Funktionswerte in die gegebene Funktionalgleichung numerisch geprüft werden und müssen es in jedem Einzelfall auch. Dazu ist zusätzlich ein Prüfprogramm vorgesehen. Nun sollen einige einfache Beispiele das Verfahren demonstrieren:

Additionstheoreme Winkelfunktionen, inklusive Vorgabewerte:

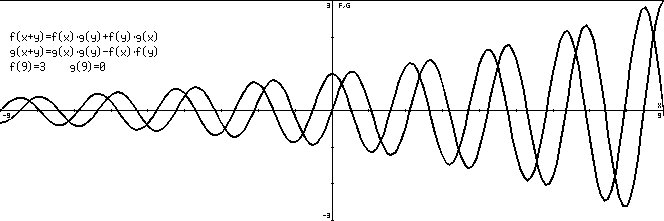
Bei anderen Vorgabewerten haben wir auch ein anderes Resultat:

Allgemeine Lösung der Additionstheorem der Winkelfunktionen ist  bekanntlich
f(x)=exp(a*x)*sin(b*x) und g(x)=exp(a*x)*cos(b*x)   mit beliebigen reellen Parametern  a,b.

Winkel_loga, inklusive Vorgabewerte:

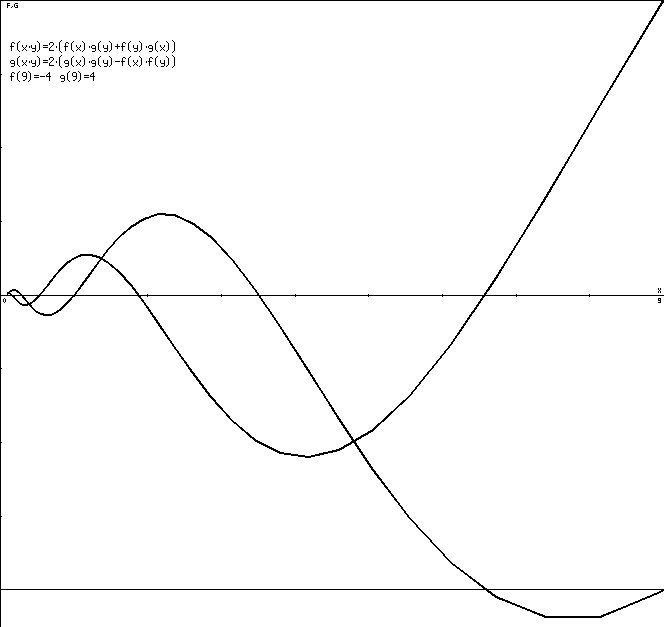
Bei Interesse kann hier das verwendete Programm samt Beispielen für HP48GX kostenlos heruntergeladen werden (rechte Maustaste), vorausgesetzt, man akzeptiert, daß keinerlei Haftung für irgendwelche Schäden übernommen wird, die im Zusammenhang mit dem Herunterladen, dem verwendeten Programm oder den Beispielen oder den Ergebnissen des Programms stehen könnten.

Um Funktionalgleichungen mit n Funktionen zu erzeugen, n>1 beliebig, können z.B. die Additionstheoreme entsprechend verallgemeinert werden:

Additionstheoreme für n Funktionen .
Bedingungen:
1. Für n=2 ergeben sich die bekannten Additionstheoreme.
2. Es gelten die oben genannten allgemeinen Voraussetzungen, z. B.
   Kommutativgesetz, Assoziativgesetz und Auflösbarkeit nach f(0).
Aus den genannten Bedingungen ergeben sich zwangsläufig die Relationen:
  f[k](x+y) = f[k](x)*f[n](y) + f[k](y)*f[n](x) ), k < n
  f[n](x+y) = f[n](x)*f[n](y) - summe ( i < n : f[i](x)*f[i](y) ) ,
  f[k](0) = 0 mit k < n und f[n](0) = 1 .

Eine numerische Lösung der so gegebenen Funktionalgleichung erfolgt hier immer nur im Intervall [ 0 , Ende ]. Die Funktionen werden im gegebenen Intervall an aufeinander mit einer Schrittweite folgender Argumentwerte berechnet.
Dabei sollen durch die berechneten Lösungsfunktionen vorgegebene Endwerte f(Ende) angenommen werden. Es sind entsprechende Startwerte f(Schrittweite) derart zu bestimmen, dass f(Ende) angenommen wird.
Dazu ein Beispiel für n=4, Schrittweite = 0.1, (Intervall)Ende = 20 und Endwerte = { 1 , -1, 3, -2 }:

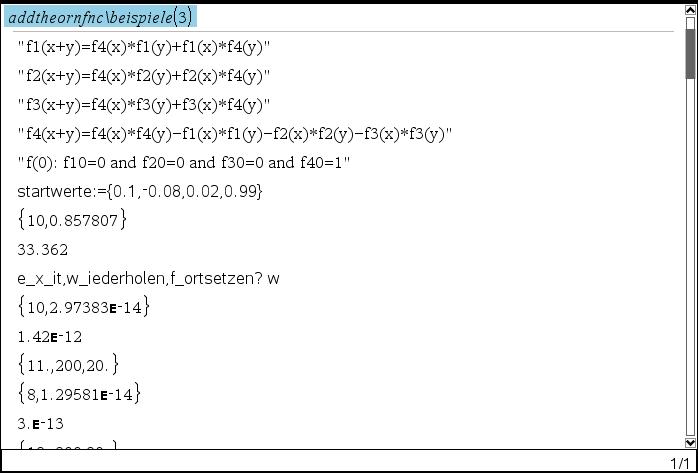
grafische Darstellung:

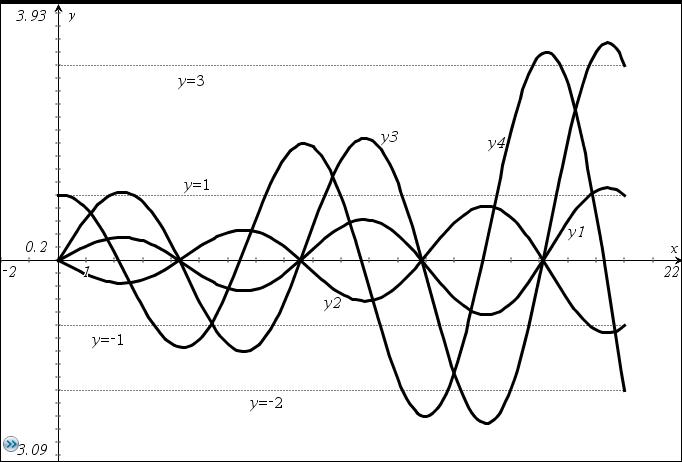
eine andere Lösung der gleichen Aufgabe:

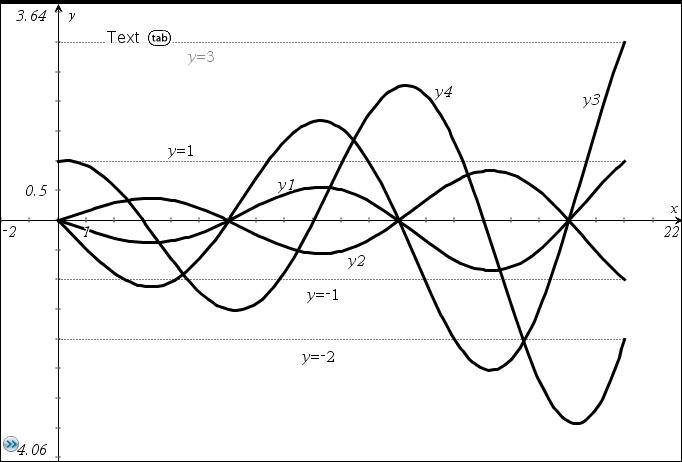
Um die Startwerte f(schrittweite) als Funktionen der Endwerte f(Ende) zu berechnen, muss das nicht lineare Gleichungssystem
Endwerte ( Startwerten ) = f ( Ende )
hier mit einem n - dimensionalen Newtonverfahren aufgelöst werden. Das gelingt allerdings nur dann, wenn die Schätzwerte für die Startwerte im Einzugsbereich einer Lösung liegen. Das erweist sich i. allg. als schwer realisierbar. Nur bei geringem Auflösungsvermögen der Aufgabe, d.h. der Quotient Ende/Schrittweite ist eine kleine natürliche Zahl, z.B. 3, 4, ... 10, sind geeignete Schätzwerte leichter vorzugeben. Bei Misserfolg muss man evtl. mehrere Versuche dazu starten.
Um ein erwünschtes Auflösungsvermögen der Lösungsfunktionen, z.B. 200 Punkte im Intervall, zu erreichen, ist ein recht aufwendiges Verfahren anzuwenden:
Ausgehend von wenigen Punkten im betrachteten Intervall, der Quotient Ende/Schrittweite sei z.B. = 3, werden für alle folgenden Auflösungen die jeweiligen Startwerte berechnet. Dabei sind die Schätzwerte einer neuen Berechnung gleich den zuletzt berechneten Startwerte. Um bei dem Beispiel von 200 Stützpunkten zu bleiben - Berechnungen für 3, 4, ..., 19, 20, 22, ..., 28, 30, 33, 36, 39, 42, 46, 50, 55, ..., 179, 196, 200. Jeweils 10% des bereit erreichten Quotienten wird zur Vergrößerung der Auflösung hinzugenommen, aber mindestens 1.
Die Lösung der Funktionalgleichung wird i.allg. veranschaulicht als Funktionen y(x), im Beispiel(2) des erwähnten TI-Programmes jedoch als Funktionen y[k](y[i]) , i<>k:

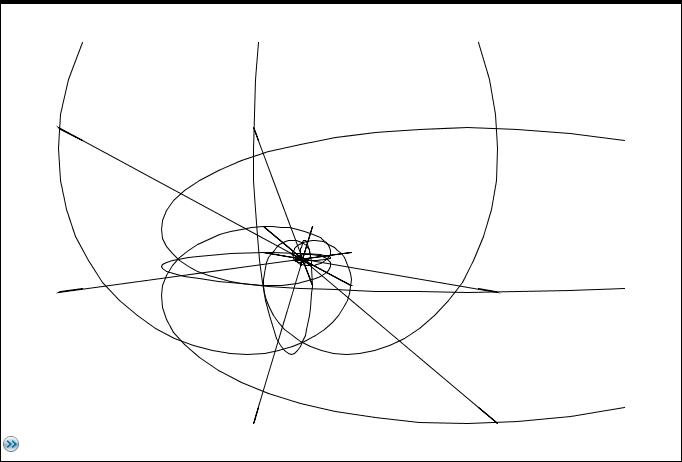
Hier noch die Lösung mit n=7 Funktionen, y(x)

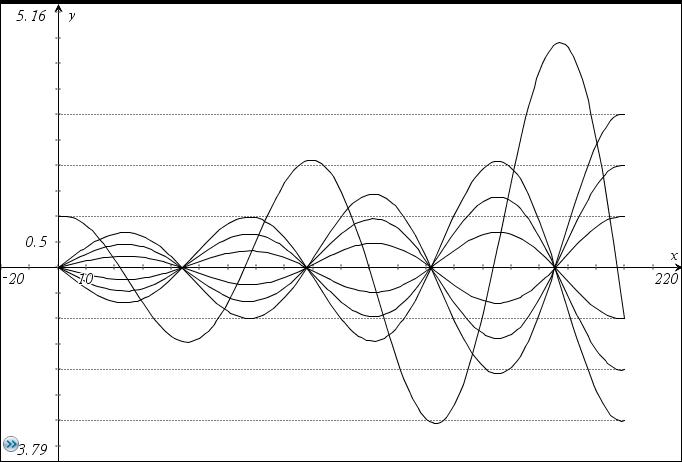
bzw. y[k](y[i]), i<>k:

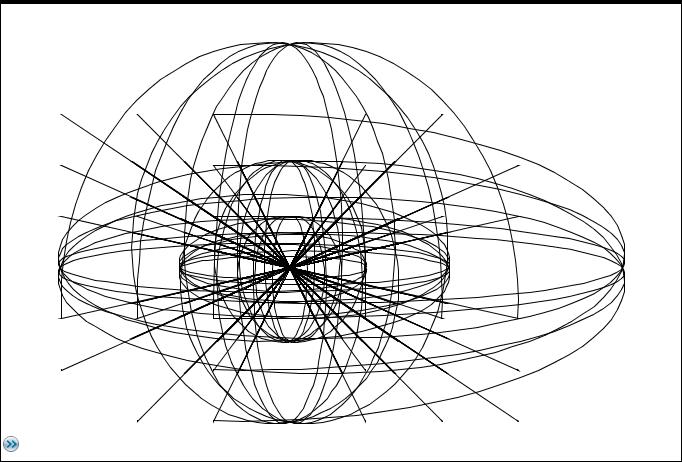
Ein entsprechendes Programm ist in der hier abrufbaren TI-Nspire-Bibliothek verfügbar.
Die Prüfung auf Zulässigkeit einer gegebenen Funktionalgleichung erfolgt dagegen in dieser Bibkliothek (für beide Progamme:Haftungsausschluss).
Zu letzterem ein Beispiel:

Der Kurvenverlauf:

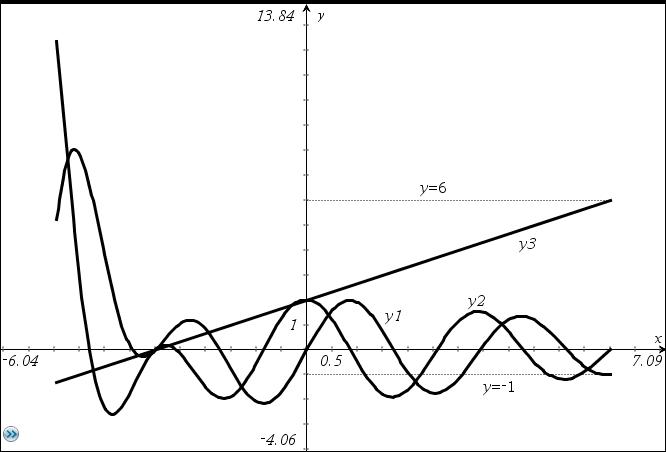
Gewöhnliche Differentialgleichungen numerisch lösen

Betrachtet werden Funktionen einer Veränderlichen und Differentialgleichungen für derartige Funktionen.
Bei einer numerischen Auflösung solcher Gleichungen werden nur Näherungslösungen gewonnen.
Als Grundlage aller weiteren Berechnungen dient die Lösung eines Anfangswertproblems.
Dabei und bei allen abgeleiteten Aufgaben sind 4 Fälle möglich:
1. Es existiert eine Lösung des gegebenen Problems und eine numerische Lösung kann gewonnen werden und approximiert eine exakte Lösung.
2. Es existiert keine Lösung des gegebenen Problems und eine numerische Lösung kann gewonnen werden und ist falsch.
3. Es existiert eine Lösung des gegebenen Problems und keine numerische Lösung kann gewonnen werden.
4. Es existiert keine Lösung des gegebenen Problems und keine numerische Lösung kann gewonnen werden.
Um numerische Lösungen zu prüfen, sollte immer ein Vergleich solcher Lösungen der gleichen Aufgabe mit unterschiedlicher Schrittweite im Lösungsverfahren vorgenommen werden, vorzugsweise mit aufeinander abgestimmten Schrittweiten (z.B. d, d/2, ...), um Berechnungspunkte geeignet miteinander vergleichen zu können. Allerdings ergibt ein derartiges Vorgehen keine Sicherheit für die Bewertung numerischer Ergebnisse, lediglich eine Plausibilität kann dabei erwartet werden. Sicherheit über das Berechnungsresultat ist immer nur in Abhängigkeit vom Hintergrund der jeweils betrachteten Aufgabe zu erlangen.
Anfangswertproblem
Gegeben sind ein Differentialgleichungssystem dgl (kann auch aus 1 Dgl. bestehen), Menge der Anfangswerte awp und Menge der Variablen vars. Dann wird mit dem Programmaufruf
numdglawp(dgl,awp,vars,d,ende,display)
das Anfangswertproblem im Intervall Anfang (erstes Element der Anfangswerte) bis ende mit der Schrittweite d gelöst.
Einige Beispiele dazu kann man z.B. hier nachlesen.
Alle berechneten Werte am Ende des Intervalls sind dann auch als Funktionen der Anfangswerte zu betrachten. Je nach Wahl der Anfangswerte kommen unterschiedliche Funktionswerte, Ableitungen usw. am Ende des Berechnungsintervalls zustande.
Dieser Zusammenhang wird sowohl bei der Berechnung von Randwerten als auch Eigenwerten ausgewertet.
Randwertproblem
Neben dem Differentialgleichungssystem dgl und den Parametern vars sind gegeben die Menge der Anfangswerte aw, die Menge vorgegebener Endwerte ew und die Menge der Schätzwerte sw. Mit dem Aufruf
numdglrwp(dgl,aw,ew,sw,vars,h,d,display)
wird das mit dgl,aw,ew,vars gegebene Randwertproblem numerisch gelöst.
Die Schätzwerte dienen dabei als Ausgangspunkt für die Anwendung eines (i.allg. mehrdimensionalen, nichtlinearen) Newtonverfahrens, um die "Endwertfunktionen der Anfangswerte" mit den Werten ew in Übereinstimmung zu bringen. Im Newtonverfahren nötige Ableitungen der "Endwertfunktionen" werden durch entsprechende Differenzenquotienten der Schrittweite h ersetzt, siehe Programmaufruf. Das Integrationsintervall ist definiert im ersten Parameter von aw bis zum ersten Parameter von ew. Die Schätzwerte betreffen nur Anfangsparameter, die in aw nicht vorkommen, demonstriert an einem Beispiel:
Definition der Randwertaufgabe



Resultat der Berechnungen


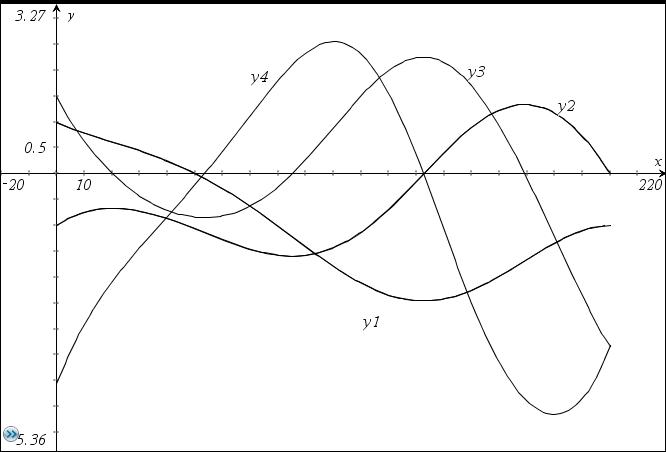
Bei ungeeigneten Schätzwerten versagt das Newtonverfahren, die Iteration wird nach 10 Schritten abgebrochen. Die Schätzwerte müssen im "Einzugsbereich einer Lösung liegen. Im nichtlinearen Fall können durchaus mehrere Lösungen existieren und auch berechnet werden. Allerdings ist die Auswahl geeigneter Schätzwerte je nach konkretem Beispiel evtl. schwierig.
Weitere Beispiele für Randwertprobleme und auch Eigenwertaufgaben findet man im TI-Nspire Programm (Achtung: Haftungsausschluss).
Eigenwertaufgabe
Gegeben sind Differentialgleichungssystem dgl, die Menge der Anfangswerte aw, die Menge vorgegebener Endwerte ew, die Menge der Schätzwerte sw und die Parameter vars. Dabei sind Einschränkungen der möglichen Angaben zu beachten: In dgl darf nur eine Differentialgleichung enthalten sein und diese muss den Parameter λ enthalten. In sw muss zusätzlich als letzte Angabe ein Anfangswert für λ definiert sein. Damit bleibt die erste Angabe in sw von jeglicher Änderung durch das Programm unberührt und definiert so die Norm einer Lösung. Während bei Randwertproblemen mehrfache Lösungen nur ausnahmsweise (und unerwünscht) vorkommen können, sind Mehrfachlösungen in Eigenwertaufgaben die Regel. Mit dem Aufruf
numdglewa(dgl,aw,ew,sw,vars,h,d,display)
wird die mit dgl,aw,ew,vars gegebene Eigenwertaufgabe numerisch gelöst.
Ein Beispiel dazu kann in der Diashow betrachtet werden.



           Substitutionsgruppe
Wir betrachten beliebig oft differenzierbare Funktionen mit dem Wert 0 für das Argument 0 und der ersten Ableitung ungleich 0 an der Stelle 0, und nehmen als Verknüpfung die Substitution
f*g = f(g(x)).
Da dabei im allgemeinen nicht die Reihenfolge vertauscht werden kann, ist die entstehende unendliche Gruppe nicht abelsch (das Assoziativgesetz muß erst noch nachgewiesen werden).
Um in dieser Gruppe mit einem Taschenrechner rechnen zu können, z.B. die Inverse oder ganzzahlige Potenzen einer Funktion zu bestimmen, gehen wir von der Taylor-Reihe der jeweiligen Operanden aus und betrachten nur deren erste n Glieder. Dabei wächst für die grundlegende Operation der Substitution mit der Anzahl n der betrachteten Summanden des "Taylor-Polynoms" der erforderliche Rechenaufwand extrem. Diesem Trend kann durch eine Festlegung des betrachteten maximalen Polynomgrades begegnet werden. In unserem Fall nehmen wir n=15. Das läßt sich gerade noch mit der Rechenkraft des Taschenrechners TI92Plus bewältigen. Dann erfolgt die Substitution durch ein für allemal fertig berechnete Formeln, die natürlich recht aufwendig mit dem gleichen Taschenrechner bestimmt und im Programm abgespeichert wurden. Der Taschenrechner hat sich dabei sozusagen selbst programmiert. Die betreffenden Formeln von Hand zu bestimmen, dürfte bei n=15 ziemlich schwierig sein.
Um den Sachverhalt zu verdeutlichen, betrachten wir als Beispiel die Potenzen sin^2(x), d.h. sin(sin(x)), und sin^(1/2)(x), d.h. eine Funktion f(x), für die f(f(x))=sin(x) gilt ( nicht zu verwechseln mit sqrt(sin(x)) ). Da wir nur Koeffizienten ohne Imaginärteil zulassen, gibt es dabei jeweils maximal zwei unterschiedliche Resultate.
Mit dem Taschen-Computer TI-Nspire ergeben sich hier: Formeln und Funktionen.
Bei der Berechnung ganzzahliger Potenzen einer Funktion, also z.B. f^3(x)=f(f(f(x))) , können wegen des Assoziativgesetzes 2^k-fache Teilpotenzen zusammengefaßt werden. D.h. z.B. zur Berechnung von f^1000 werden f,f^2=f*f,f^4=f^2*f^2,f^8=f^4*f^4,...,f^512=f^256*f^256 gebildet und die erforderliche Auswahl geeigneter Potenzen gemäß Binärdarstellung von 1000 zu f^1000 zusammengesetzt. Für große Potenzen entstünde andernfalls ein unnötiger Rechenaufwand. Im hier betrachteten Programmsystem für den TI89/TI92+ ist als maximale Potenz 1023 festgeschrieben.
Neben der Invertierung von Funktionen werden auch rationale Potenzen von Funktionen als interessant betrachtet.

Beispiel: sin^(9/10)(x) ist die Funktion f(x) mit der Eigenschaft
sin(sin(sin(sin(sin(sin(sin(sin(sin(x)))))))))=f(f(f(f(f(f(f(f(f(f(x))))))))))
    
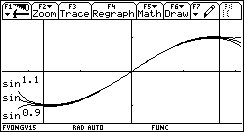
Allerdings muß dabei immer beachtet werden: Sofern eine derartige Funktion mit den geforderten Eigenschaften existiert, werden die ersten n=15 Glieder der Taylor-Entwicklung um den 0-Punkt bestimmt, andernfalls haben die gewonnenen Koeffizienten keine Bedeutung.

Bei Interesse kann hier das verwendete Programm samt Beispielen für TI89/TI92+ kostenlos heruntergeladen werden (rechte Maustaste), vorausgesetzt, man akzeptiert, daß keinerlei Haftung für irgendwelche Schäden übernommen wird, die im Zusammenhang mit dem Herunterladen, dem verwendeten Programm oder den Beispielen oder den Ergebnissen des Programms stehen könnten.

           Kompositionsgruppe

           Polynome mit mehreren Variablen

           Numerik-ARABIAta

           Lineare Optimierung
Wenn man Aufgaben der linearen Optimierung korrekt auf einem Rechner zur Lösung bringen muß, führen Rundungsfehler beim Rechnen mit Gleitkommazahlen zu fehlerhaften Resultaten. Eine Anwendung von CAS-Rechnern (Computer-Algebra-System) liegt daher nahe. Z.B. bietet der neue Taschencomputer TI-Nspire CAS entsprechende Möglichkeiten. Hier wurde ein existierendes Programm-Paket vom TI 92+ auf den Nspire übertragen. Allerdings mußte auf Teile des Programms verzichtet werden, weil im TI-Basic (noch?) nicht alle Befehle auf dem Nspire bereitstehen. Trotzdem kann auch mit der verkleinerten Version des Programms zur Linearen Optimierung erfolgreich gearbeitet werden. Und vorteilhaft, da der TI-Nspire CAS im TI-Basic um ein Vielfaches schneller rechnet als der TI 92+.
Voraussetzungen für die Programmanwendung:
1) Alle auftretenden Funktionen sind linear.
2) Die Zielfunktion der Optimierung ist - gekennzeichnet durch -
a) Maximum - "maxi",
b) Minimum - "mini",
c) alle Lösungen im Maximum - "maxivoll",
d) alle Lösungen im Minimum - "minivoll".
3) Alle auftretenden Nebenbedingungen enthalten ihren Rand ( =,<=,>=, nicht jedoch <,> ).
4) Alle auftretenden Variablen (x1,x2,...) sind (nicht negativ, also) >=0.
Die letztere Bedingung stellt nicht wirklich eine Einschränkung dar. Soll z.B. die Variable x7 auch negative Werte annehmen, muß man nur eine zusätzliche Variable x33 einführen, x33 sei dabei die ersten in der Aufgabe nicht verwendete Variable, und folgende Schritte vollziehen:
1) In allen Relationen der Aufgabe, also in der Zielfunktion und in den explizit aufgeführten Nebenbedingungen, die Größe "x7" durch "substitut" ersetzen.
2) In allen Relationen der Aufgabe die Größe "substitut" durch den Ausdruck "(x7-x33)" ersetzen.
Beide Substitutionen gelingen leicht mit der Funktion | im TI-Nspire-Basic.
Natürlich muß man sich merken, daß die Zusatzvariable x33 als Negativwert von x7 in Erscheinung tritt. Im Programm linopt tritt gegebenenfalls im Resultat noch ein Parameter t1 (usw.) auf, den man bei vorhandenem Optimum getrost ignoriert.
Der geschilderte Vorgang ist für alle Variablen x zu wiederholen, für die auch negative Werte zugelassen werden sollen.
Anschließend kann die Berechnung beginnen.
Im vorliegenden Programm werden einige Beispiele (1 bis 13) bereitgestellt, um auf unterschiedliche Fälle bei der Linearen Optimierung hinzuweisen.
Schritte der Programmausführung:
1) Ermittlung einer "zulässigen Ecke" (existiert sie nicht, gibt es keine Lösung).
2) Berechnung der optimalen Zielfunktion (Maximum oder Minimum).
a) Berechnung einer Lösung,
b) Berechnung aller Lösungen ("maxivoll","minivoll").
3) Berechnung aller Eckpunkte des (durch die Nebenbedingungen definierten) Simplex.
Dazu muß die gegebene Zielfunktion nur durch die "neutrale" Zielfunktion ersetzt werden:
"minivoll=0" bzw. "maxivoll=0".
Das vorliegende Programm stellt auch Sonderfälle fest. Z.B. kann das Simplex einseitig offen sein. Dann kann je nach Zielfunktion trotzdem ein Optimum existieren, oder auch nicht. Alle derartigen Fälle werden sinngemäß erkennbar festgestellt und ausgewertet.
Hier folgt nun ein einfaches Beispiel. Mit der "neutralen" Zielfunktion erhält man alle Punkte des Simplex.
Bei der Darstellung der Kanten

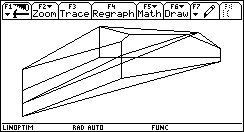
wird eine Projektion eines höher dimensionalen (im Beispiel 4-D) Raumes in eine 2-D-Ebene vorgenommen. Das Ergebnis erscheint ziemlich unübersichtlich. Zur Vereinfachung der Abbildung blenden wir alle verdeckten Kanten aus. Das Bild oben sieht nicht danach aus. Aber man muß immer an die hier 4 Dimensionen des Originals denken, wenn man die Abbildung richtig verstehen will.
Die Beispiele 1 bis 13 und das Programm zur Linearen Optimierung können hier kostenlos auf eigene Gefahr herunter geladen werden. Es wird keine Haftung für Schäden übernommen, die im Zusammenhang damit irgendwie auftreten könnten.
Achtung: Betriebssystem Version 3.02# des TI-Nspire CAS.



           Freiformflächen und Zwangsbedingungen
Abweichend vom allgemein bevorzugten Verfahren soll hier die Freiformfläche ausschließlich durch Punkte definiert werden. Um das zu ermöglichen, muß eine sukzessive Vergrößerung der in einem Rechteckschema gegebenen definierenden Punktmenge mittels Ergänzung durch geeignet positionierte Zwischenpunkte vorgenommen werden. Die Qualität der Flächendefinition ergibt sich dabei aus der Positionierung der Zwischenpunkte.
Das vorliegende Verfahren zur Positionierung der Zwischenpunkte ist hier besonders einfach gewählt. Genauer, aber auch wesentlich aufwendiger wäre die simultane Berechnung der Zwischenpunkte nach dem Minimum der Summe der Quadrate der zweiten Abstandsdifferenzen über dem Rechteckschema aller Punkte. Das führt zu einem großen, nicht linearen Gleichungssystem für alle Punktkoordinaten (x,y,z) aller Zwischenpunkte.
Eine deutliche Verringerung des Rechenaufwandes ergibt sich beim Übergang von der Fläche zu ihren Parameterkurven. Dann müssen zwar alle Parameterkurven berechnet werden (und sogar zweimal, wegen der Reihenfolge erst x, dann y und umgekehrt), aber bei jeder (Raum)Parameterkurve sind nur ihre Punkte und Zwischenpunkte im zugeordneten nicht linearen Gleichungssystem enthalten.
Jedes der genannten nicht linearen Gleichunssysteme kann mittels mehrdimensionalem Newtonverfahren gelöst werden. Als Startwerte wären dabei die im oben erwähnten Einfachverfahren gewonnenen Punkte geeignet:
Das Verfahren ergibt sich, wenn die Koordinaten der räumlichen Parameterkurven separat betrachtet werden und die Quadratesumme der zweiten Differenzen der Koordinatenwerte zum Minimum gemacht wird. Dann resultiert für jede Komponente in jeder Parameterkurve ein einfaches lineares Gleichungssystem zur simultanen Berechnung der Komponenten der Zwischenpunkte der Parameterkurve. Dabei sind in jeder Gleichung mit Ausnahme der ersten und der letzten nur drei Koeffizienten ungleich 0: 1, 6, 1. Die Koeffizienten folgen aufeinander und 6 steht in der Hauptdiagonalen.
Jetzt ist der Aufwand so gering, daß mehrfach alle Zwischenpunkte gesetzt werden können. Durch mehrere Verdichtungen der Punktmenge kann die Freiformfläche immer genauer erfaßt werde.
Auf eine derartige Punktmenge kann (in jedem Verdichtungsschritt) eine Bedingung zur Punktlage angewandt werden. Diese Zwangsbedingung kann auf Bereiche in ihrer Wirkung eingeschränkt und auch bezüglich der Positionierung der Punkte ziemlich willkürlich sein.
In einer grafischen Darstellung wird dann deutlich, ob die Zwangsbedingung zur Freiformfläche paßt oder nicht.
Mit dem beschriebenen Verfahren können vorteilhaft zwei unabhängige Vorgaben, zum einen eine Punktmenge als Freiformfläche, zum anderen eine (evtl. vielfach gegliederte) Funktion von (x,y,z) als Zwangsbedingung, zur Beschreibung eines geometrischen Ortes benutzt werden.
Und der geringe Aufwand erlaubt sogar eine Implementierung auf einem Taschenrechner, hier dem TI-Nspire. Das entsprechende Programm Freiformflaechen.tns kann kostenlos heruntergeladen werden, sofern man Haftungsausschluß akzeptiert. Es wird keinerlei Haftung für Schäden im Zusammenhang mit dem genannten Programm übernommen.
Mit dem Programm wurde auf dem TI-Nspire ein sehr einfaches Beispiel (Fläche 4x4 Punkte, Zwangsbedingung Kugel) gerechnet und hier in einem einfachen Video dargestellt.

Mit dem PC sollte ein etwas detailreicheres Beispiel (hier eine Diashow) gelingen:
Freiformfläche - 5 x 8 = 40 Punkte
Zwangsbedingung - 2 Ebenen und 4 Flächen zweiter Ordnung (Ellipsoide).

Vergrößerung von Pixel-Bildern
Ähnlich wie bei den zuvor beschriebenen Freiformflächen werden auch hier systematisch Zwischenpunkte gesetzt, um das jeweilige Bild zu vergrößern. Allerdings muß die entstehende Datenmenge durch Auswahl von Ausschnittvergrößerungen begrenzt werden. Ein weiterer wichtiger Unterschied zu den Freiformflächen ergibt sich, weil zur Berechnung der Zwischenwerte ausschließlich die unmittelbare Umgebung des eingefügten Punktes herangezogen wird. Im vorliegenden Fall sind es jeweils die 16 unmittelbaren Nachbarpunkte. Auch unter dieser Voraussetzung gibt es viele unterschiedliche sinnvolle Möglichkeiten einer Berechnung der Zwischenwerte. Sogar zeigte sich an verschiedenen Beispielen die Abhängigkeit der Effizienz eines Formelsatzes vom umgebenden Bildinhalt. So ist doch noch ein Einfluß einer weiteren Umgebung auf die Berechnung eines Zwischenpunktes gegeben, weil in einem Berechnungsverfahren unterschiedliche Formeln verwendet werden, je nach erkannten Eigenschaften der Bildumgebung.
Trotz solcher Bemühungen kann die Vergrößerung eines Pixel-Bildes nur mäßigen Ansprüchen genügen. Das wird auch in dem kleinen Beispiel deutlich, das man mit einiger Phantasie als "Seeigel und kleine Quallen im Wrack" bezeichnen kann.
Ein weiteres Beispiel beinhaltet die Identifizierung einfacher Objekte in einem Pixelbild sowie die Pixelbild- und parallel dazu die Objektvergrößerung.
Als Ausgangsbild dient Nummer 1750 aus dem Video zur Explosion eine Supernova, die Objekte sind Kugeln. Es entsteht eine Bildfolge
"Wolken und Kugeln"



Komponenten der CORIOLIS-Beschleunigung (auf der Erdoberfläche)
RS - Ruhe System, BS - bewegtes System, hier die rotierende Erde mit ω = [0, 0, 1] *2*π/_day .
Bei vr - Relativgeschwindigkeit eines Körpers (gegen BS) ergibt sich die CORIOLIS-Beschleunigung ac = 2*ω x vr .
Sei α - Winkel zwischen ω und vr , so resultiert |ac| = 2*|ω|*|vr|*sin(α).
Ist ρ die geografische Breite, so ergeben sich die Komponenten der CORIOLIS-Beschleunigung bezüglich der Basisvektoren des BS zu einem gegebenen Zeitpunkt:
   [1, 0, 0] - Richtung OST ,
   [0, -sin(ρ), cos(ρ)] - Richtung NORD (SÜD) ,
   [0, cos(ρ), sin(ρ)] - Richtung ZENIT.
Die Komponenten sind mit
vr = [1, 0, 0] *vx + [0, -sin(ρ), cos(ρ)] *vy + [0, cos(ρ), sin(ρ)] *vz , d.h.
ac = [vy*sin(ρ)-vz*cos(ρ), vx, 0] *4*π/_day bei Projektion auf die Basisvektoren
ac = ( [1, 0, 0] * (vy*sin(ρ)-vz*cos(ρ)) +
           [0, -sin(ρ), cos(ρ)] * -vx*sin(ρ) +
           [0, cos(ρ), sin(ρ)] * vx*cos(ρ) ) * 4*π/_day.
Darstellung in Basisvektoren
ac = [(vy*sin(ρ)-vz*cos(ρ)), -vx*sin(ρ), vx*cos(ρ)] *4*π/_day .
Falls vz = 0, ergibt sich in der Horizontebene ac = [vy, -vx, 0] *sin(ρ)*4*π/_day .
So in den Programmen coriolisabdrift und windfeld auf dem Taschencomputer TI-Nspire (Haftungsausschluss) verwendet.
Hier eine Anwendung von windfeld(54°,10.5*_knot,-2.5*_knot,10*_hr,1*_s) (links)
und von windfeld3d(54°,10.5*_knot,-2.5*_knot,0*_knot,10*_hr,1*_s) (rechts) im Grund- und Aufriss:

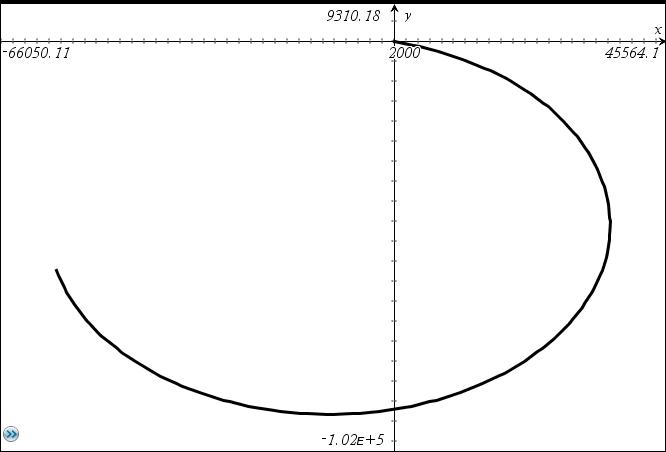
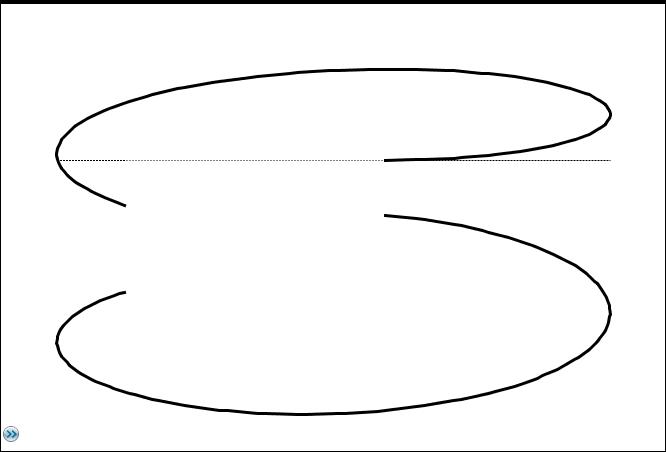
Die Komponente vz beeinflusst den Luftdruck , vz > 0 , der Druck fällt, vz < 0 , der Druck steigt.
Bei andauerndem Westwind, vx > 0, steigt vz an und der Luftdruck fällt. Umgekehrt, bei andauerndem Ostwind, xv<0, fällt vz und der Luftdruck steigt.
Die Anwendung druck3d(54°,10.5*_knot,-2.5*_knot,0*_knot,10*_hr,1*_s) zeigt das in der folgenden Abbildung,
blau - der Druck steigt, rot - der Druck fällt:

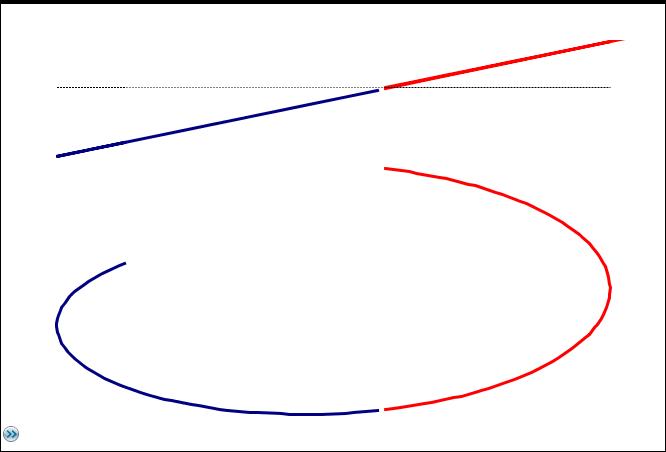
Die Wetterentwicklung hängt von vielen Faktoren ab. Darunter ist auch die CORIOLIS-Beschleunigung. Z.B. stellt sich die Windrichtung in Zyklonen auf der Nordhalbkugel linksdrehend ein: Am Umkehrpunkt des Umlaufsinnes, an dem sich die bezogen auf das Zentrum radialen Komponenten der CORIOLIS-Beschleunigung und der Druckdiffenzbeschleunigung gegenseitig kompensieren, wechselt die vorwiegende Windrichtung das Vorzeichen, Drehrichtung gegenläufig.
In einem weitgehend vereinfachten Verfahren zur Luftbewegung in einem Zyklon im Programm
tiefdruckgebiet(54°,800*_km,((0.1*_m)/(_s^(2))),20*_hr,2*_s) wird die Bewegung von einzelnenen Punkten über einen Zeitraum beobachtet. Die jeweilige Anfangsgeschwindigkeit ist 0. Die maximale, durch die Druckdifferenz bedingte Beschleunigung nimmt mit dem Abstand vom Zentrum linear ab und wird zusätzlich proportional zu cos(α), α der Winkel zwischen Windrichtung und Radius, und der Windgeschwindigkeit wegen Verwirbelung reduziert. Die Windgeschwindigkeit unterliegt außerdem einer durch Reibung bedingten Verringerung.
Hier eine entsprechende Abbildung:

Bei großer Windgeschwindigkeit im Verhältnis zum Luftdruckgefälle bewirkt die Fliehkraft das Auge des Sturms:

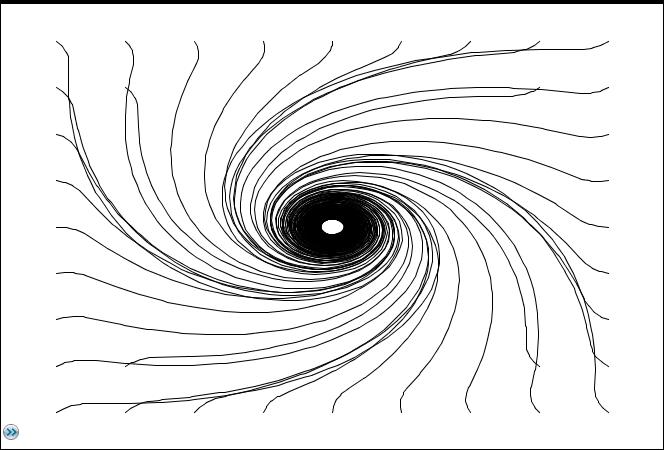
Weitere Beispiele :
Z.B. h = 80_m, t= √(2*80_m/_g), v = h/t , ac = (π/1080)*(_m/_s^(2)) , Weg ≈ (1/2)*ac*t^(2) = 0.023_m
Z.B. Auslenkung, am Äquator=0, am Pol maximal (N nach rechts, S nach links).
Z.B. Gewehrkugel mit 500_m/_s Anfangsgeschwindigkeit nach 1_s und 500_m um 0.028_m nach rechts abgelenkt.
Z.B. Eisenbahn, Belastung der Gleise, im Norden immer die in Fahrtrichtung rechte, im Süden die Innenseite der linken Schiene.


Loxodrome & Orthodrome



Die Orthodrome (Großkreis) ergibt die kürzeste Entfernung. Allerdings muss auf ihr der Kurs ständig neu bestimmt werden. Das erfordert einige Berechnungen. Zum einen sind die Koordinaten(λ,φ) der jeweiligen neuen Position zu bestimmen und anschließend der zugeordnete neue Kurswinkel α gegenüber Nord. Der Kurs ergibt sich dabei als Funktion der aktuellen Position gegenüber der Zielposition(λ2,φ2). Dieser Vorgang beginnt beim Start(λ1,φ1) und wird mit einer (kleinen) Schrittweite für die Entfernungsdifferenz aufeinander folgender Positionen vollzogen. In einem kleinen Programm für den Taschencomputer TI-Inspire CAS werden die Zwischenpositionen alle 4_Nmil (nautische Meilen) berechnet und die Positionen mit jeweiliger neuer Kursangabe alle 40_Nmil auf dem Display angezeigt. In dem betreffenden Programm (hier, Haftungsausschluss) sind auch einige Beispielorte angegeben (die Liste kann jederzeit nach Bedarf erweitert werden).
Hier nun der Kurs für eine Orthodrome von Algier nach Auckland in einem λ-φ-Diagramm:



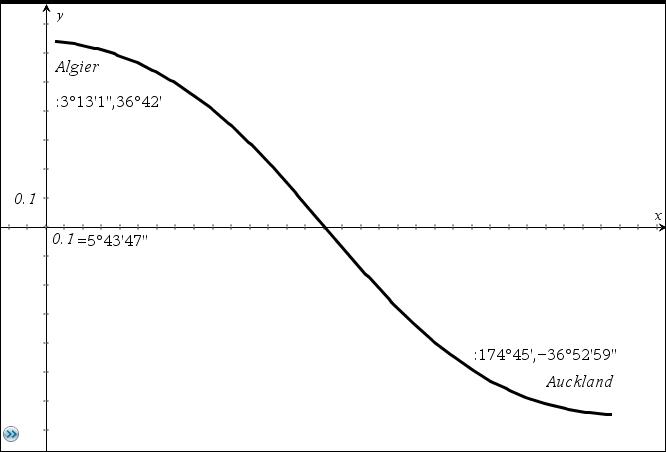
           Transformiere gleichverteilte Pseudozufallszahlen in normalverteilte
Gleichverteilte Pseudozufallszahlen sind auf diversen Taschenrechnern und in verschiedenen gängigen Programmiersprachen verfügbar und zu Zwecken der Simulation auch nützlich. In manchen Fällen sind allerdings normalverteilte Zufallszahlen für eine Modellierung erforderlich. Es genügt dabei, standardnormalverteilte Zufallszahlen bereitzustellen, da eine Verschiebung des Erwartungswertes und eine Streckung mit der Streuung einfach zu vermitteln sind. An Stelle einer direkten Erzeugung soll hier die Transformation der vorhandenen gleichverteilten Zufallszahlen in standardnormalverteilte vorgenommen werden. Dazu vergleichen wir die Verteilungsdichte in beiden Fällen, x gleichverteilt im Intervall [-1,1] und y standardnormalverteilt. Die Integrale über die Verteilungsdichten von 0 bis x bzw. von 0 bis zur Transformierten y müssen gleich sein:

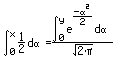
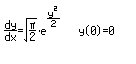
Bei der numerischen Bestimmung der Funktion y(x) mit Hilfe der Differentialgleichung beachten wir die Relation y(-x)=-y(x) und beschränken uns auf das Intervall [0,1). Eine erforderliche Genauigkeit von .000001 kann dabei eingehalten werden. Allerdings ist die entstehende Rechenzeit im Fall einer wiederholten Anwendung zu groß. Man muß bedenken, daß Simulationen, z.B. Monte Carlo Methoden, die Erzeugung sehr vieler Zufallszahlen erforderlich machen. Daher liegt nahe, eine nach Intervallen eingeteilte numerische Repräsentation der Transformationsfunktion zu verwenden. Im vorliegenden Beispiel ist der Bereich [0,.999] mit der obigen Genauigkeit erfaßt, im Intervall (.999,1) nimmt die Genauigkeit stark ab. Bei Bedarf kann durch Anfügen weiterer Koeffizienten der Genauigkeitsbereich ausgedehnt werden, ohne den Rechenaufwand zu vergrößern, lediglich die Länge der Funktion nimmt zu. Hier nun die Programmliste für den HP48GX, eine Übertragung in eine andere Programmiersprache wird durch die Angabe der Liste auch ohne HP48GX ermöglicht:

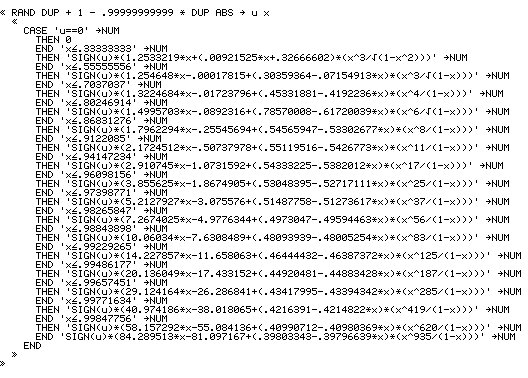
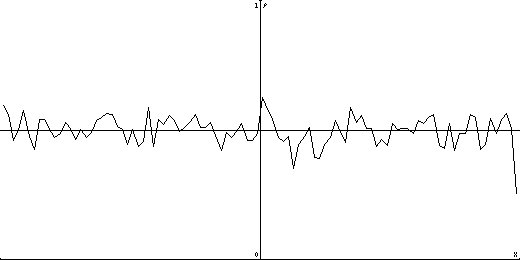
Zur Verdeutlichung der Unterschiede zwischen gleichverteilten und standardnormalverteilten Zufallszahlen erfolgen nun die grafischen Darstellungen der konkreten Verteilungsdichten bei je 10000 Pseudozufallszahlen mit dem HP48GX. Im ersten Bild mit einer Auflösung von .02, gleichverteilt:

Im zweiten Bild mit einer Auflösung von .1, standardnormalverteilt:

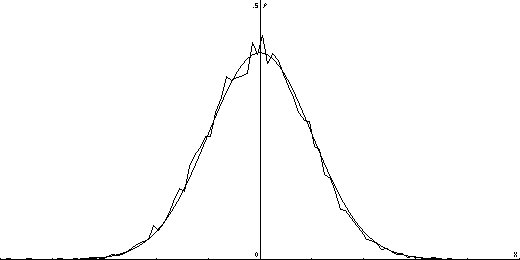
Hier wurde das Teilintervall [-5,5] gewählt.

Numerische Berechnung des Wilcoxon-Zwei-Stichprobentest

Betrachtet werden 2 Gruppierungen A und B. Eine entsprechende Berechnung für bis zu 100 Zufallsstichproben je Gruppierung soll mit dem Taschencomputer TI-Nspire CAS ermöglicht werden. Dazu sind folgende Funktionen zu implementieren:

1. Anzahl der Inversionen der Gruppierungen A und B

Durch paarweisen Vergleich der Elemente von A und B nach ihrer Größe wird die Anzahl der Inversionen ermittelt.

2. Berechnung des Rückweisbereiches < u von m, n und Wahrscheinlichkeit α

Der Rückweisbereich wird mit Hilfe einer Funktion w(u, m, n) der Anzahl aller Anordnungen von Werten in A und B mit höchstens u Inversionen bestimmt. Es ergibt sich die Relation

α > w(u, m, n) / Binomialkoeffizient(m + n, n) .    (1)

3. Berechnung der Funktion w(u, m, n)

Mittels vollständiger Induktion gewinnt man für w die Rekursionsformel

w(u, m, n)=0 für u < 0,

w(0, m, n)=w(u, 0, m)=w(u, m, 0)=1 und      (2)

w(u, m, n)=w(u-n, m-1, n)+w(u, m, n-1) .


Wie man in (2) sieht, verzweigt sich die Rekursion für w, die Werte von w werden teilweise sehr groß und der Rechenaufwand übersteigt bereits für mäßige Werte u, m und n die Rechenkraft des Taschencomputers TI-Nspire CAS bei weitem.

Es ergibt sich ein Dilemma: Die genaue Arithmetik des TI-Nspire CAS wäre zur genauen Verarbeitung der großen Werte der Funktion w geeignet, seine Rechenkraft jedoch nicht (das gilt auch für den TI-Nspire-Interpreter am PC), die Rechenleistung eines einfachen PC reicht durchaus, jedoch dort nicht die (doppelte) Genauigkeit bei Verwendung üblicher Programmiersprachen.

Daher ergibt sich als Resultat einer Vorbereitung der Taschencomputerfunktion nur eine numerische Näherung des Berechnungsverfahrens am TI-Nspire. Das jeweilige Testergebnis nach Wilcoxon wird nur als Wahrscheinlichkeitsintervall angezeigt, bei kleinen m und n ausnahmsweise als genauer Wert.

Hier kann die Bibliothek wilcoxon für das Verzeichnis MyLib im TI-Nspire CAS herunter geladen werden. Achtung: Haftungsausschluss.

Es folgt ein Beispiel einer typischen Berechnung am Taschencomputer TI-Nspire CAS mit den Bibliotheksfunktionen inversionen, wilcoxon2 und interpol :

4. Aufbereitung der relevanten Daten am PC

Zuerst wird ein 3-D-Feld doppelter Genauigkeit w(u, m, n) mit den simultan berechneten Werten der gleichnamigen Funktion gespeichert. Die Feldgrenzen liegen bei m, n <= 100 und u <= 100*100/2. Der letzte Wert ergibt sich, weil keine Wahrscheinlichkeiten über 50% betrachtet werden. Wie man leicht nachrechnet hat dieses Feld ca. 400 MByte Speicherbedarf.

Trotz seiner Größe ist es mittels der Formel (2) schnell berechnet. In ihm sind die Funktionswerte von w(u, m, n) allerdings nur mit doppelt genauen reellen Zahlen erfasst. Für größere Indizes (u, m, n) fehlen daher die hinteren Ziffern. Damit ergibt sich eine erste Ungenauigkeit in der Datenaufbereitung am PC.

In einem zweiten Bearbeitungsschritt werden nun zu einem jeweils ausgewählten Wahrscheinlichkeitswert α mit Hilfe der Relation (1) aus dem Feld w(u, m, n) die maximalen Werte u zu betrachteten aktuellen Indizes i <= m und j <= n bestimmt und in dem α zugeordneten integer Feld u(m, n) gespeichert. Diese Felder sind jeweils 40 KByte groß und könnten daher auch auf den Taschencomputer übertragen werden.

Der genannte Vorgang wurde für α = 0.1%, Schrittweite =0.1 % bis 10% wiederholt. Bei Übertragung der entsprechenden u-Felder auf den Taschencomputer wären so bereits die Rückweisbereiche für jeden der genannten Werte α gegeben. Natürlich immer nur bis auf einen (kleinen) Fehler, der aus der Ungenauigkeit von Teilen des Feldes w(u, m, n) resultiert.

Der Abschluss der Datenaufbereitung ergibt sich aus dem Vorhaben einer (beinahe, d.h. Schrittweite 0.1%) kontinuierlichen Bestimmung des Rückweisbereichs bezogen auf die Wahrscheinlichkeit α.

Dazu wird jedes (α zugeordnete) Feld u(m, n) interpoliert. Als Interpolationsfunktionen bieten sich wegen der Symmetrie u(i, j) = u(j, i) Potenzen von (i + j), (i * j) und für gerade Potenzen (i – j) an: Potenz = 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5. So ergeben sich 19 Funktionen und jedem Feld u von α sind 19 Koeffizienten zugeordnet. Die Ungenauigkeit der Interpolation über dem gesamten Feld u von α ist mit Abweichungen von +/-1 bei ca. 1% der Indizes (i, j), ausnahmsweise +/-2 in Einzelfällen bei kleinem α, unbedeutend und wird in den oben genannten Funktionen interpol und wilcoxon2 beachtet. Bei Übertragung der Koeffizienten ergibt sich allerdings eine zusätzliche Ungenauigkeit wegen der geringeren Genauigkeit der Gleitkommazahlen am Taschencomputer, 2 Ziffern (von ursprünglich 16) gehen verloren.

Für genaue Wahrscheinlichkeitswerte muss das Feld w(u, m, n) auf dem CAS-Rechner TI-Nspire selbst erzeugt werden. Da das nur einmal am Anfang aller Berechnungen betrachteter Beispiele erfolgt, kann man die nötige Rechenzeit für mittlere Dimensionen der Gruppierungen A bzw. B hinnehmen (z.B. Dimension von A bzw. B <=20).
In einer entsprechenden Bibliothek wilcoxgenau sind neben den oben erwähnten Funktionen die Programme initwumn(maxmn) und loeschen zur Erzeugung bzw. Vernichtung der Datenstruktur wumn = w(u, m, n) vorhanden. Beide Programme können auch direkt in wilcoxgenau aufgerufen werden (empfohlen).
Die Bibliothek wilcoxgenau kann hier herunter geladen werden (Achtung: Haftungsausschluss).



"Fourier"-Interpolation

Gegeben sei ein Intervall [von,bis] und in ihm eine Folge von genauen Werten z[i] mit wenigen Elementen, gesucht ein die Werte interpolierendes "Fourier"-Polynom:

Bei einer Folge von Punkten mit mehreren Komponenten wird jede Komponente für sich als Funktion über dem Punktindex betrachtet. So z.B. bei der Erzeugung eines Videos zur Darstellung einer Interpolation von 10 Punkten in der Ebene unter dem Einfluss der Größe pot; das Video wurde mit der im obigen Text unten angegebene Funktion nach "Augenmaß" erzeugt. (Achtung: Einstellungen - Allgemein - Angezeigte Ziffern=Fließ 12, Berechnungsmodus=Auto.)
Die Größe pot, ein zusätzlicher Parameter neben den Koeffizienten ak,bk,ck, kann auch durch eine zusätzliche Bedingung berechnet werden, z.B.:
Minimum (pot) = ( Integral f1^2 )*( Integral f2^2 ) , f1=Ableitung fourier, f2=Ableitung f1, Integrale über [von,bis]
oder, ähnlich wie in "Freiformflächen und Zwangsbedingungen ", s.o.,
Minimum (pot) = ( Summe f1^2 )*( Summe f2^2 ), Argument=von,bis,Schrittweite=0.5.
Im Video wurde für beide Punktkomponenten, x,y, die gleiche Größe pot verwendet - eine Ausnahme, möglich bei dem gegebenen Beispiel.
Hier folgt nun ein Beispiel für die Berechnung der Größe pot in Abhängigkeit von 14 zufälligen Werten z[i]:

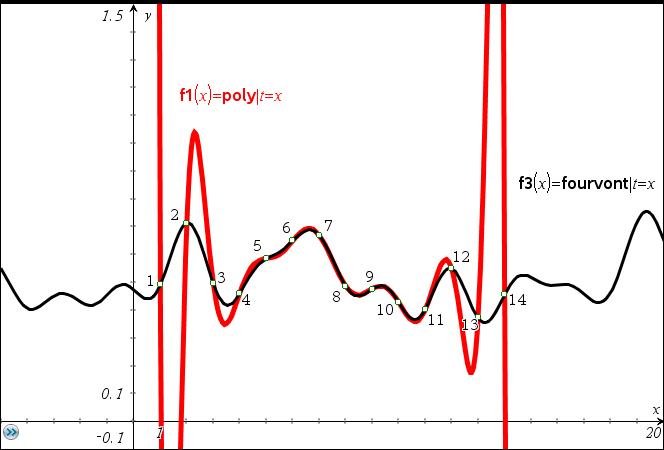
Dabei wurde an Stelle der Potenzen pot^(k-1) ein Vektor pot[k],k=1,max(nc,ns) in die Funktion Fourier eingeführt. So wurde aus einem zusätzlichen Parameter zur Bestimmung des Minimum(pot) ein Vektor von Parametern. Um pot bzw. pot[k] zu bestimmen, ist die Gleichung
0 = Ableitung Minimum(pot) nach pot bzw. das Gleichungssystem
0 = Ableitungen Minimum(pot[k]) nach pot[k] aufzulösen. Im Beispiel ergibt sich der Vektor
pot={1.008,0.706,0.6231,0.106499,0.510396,0.52679}.
In der Abbildung wurde zum Vergleich das entsprechende Interpolationspolynom Rot und mit dickem Strich dargestellt.
Nun zur Funktion fourier(z). Hier die Liste für den Taschencomputer TI-Nspire CAS:

Es macht wirklich Spaß, das kleine Programm an unterschiedlichen Beispielen auszuprobieren.
Betrachten wir noch mal das Beispiel aus dem Video:
x[i]:=2.*cos(((7.*π*(i+3.))/(30.)))-2.*cos(((7.*π*(i+3.))/(15.)))+((i)/(3.))
y[i]:=2.*sin(((7.*π*(i+3.))/(30.)))-2.*sin(((7.*π*(i+3.))/(15.))) ,
jetzt aber mit 15 Punkten und im Intervall [-2,18], und berechnen nach der oben angegebenen Bedingung für jede Komponente gesondert die Größe pot.
Es resultieren potx = 0.69854155099829 und poty = 0.71967234616316 mit der Darstellung:

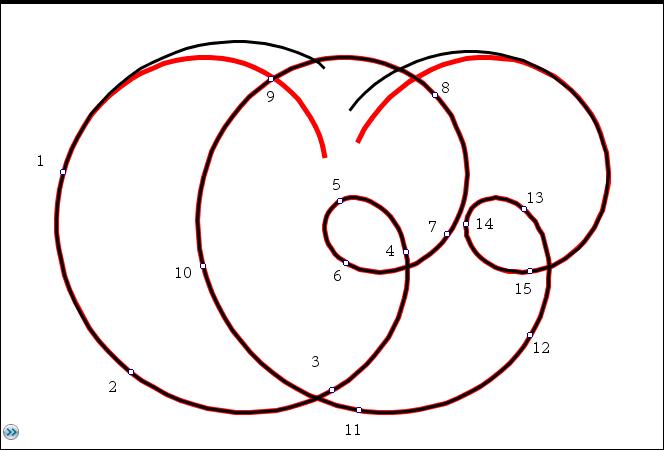
Rot und mit dickem Strich wurde zum Vergleich die Funktion zur Erzeugung der gegebenen Punkte dargestellt.
Im vorliegenden Fall kann sogar (im begrenzten Rahmen) eine Extrapolation von Werten erfolgen - als eine Prognose über den angrenzenden Bereich zu [1,15].
Überflüssig zu bemerken, dass das betrachtete Beispiel mit echter Fourierinterpolation exakt dargestellt wird,
Zum Abschluss nochmals das gleiche Beispiel, jedoch mit zufallsgestörtem Argument. Zum Vergleich kann daher auch nur das Interpolationspolynom herangezogen werden (rot, dicker Strich):


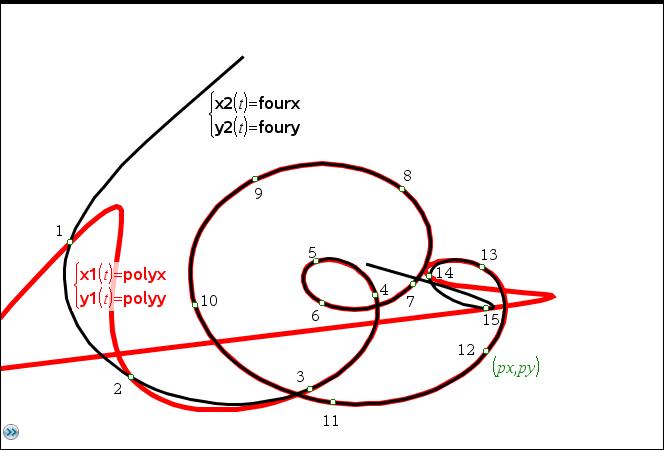
Anmerkung:
Bei großen Unterschieden der Abstände aufeinander folgender Vorgabepunkte in ihrem Darstellungsraum leidet die Qualität einer Interpolation. Daher kann ein Einfügen von zusätzlichen Punkten in den größten Lücken vorteilhaft sein.
Insgesamt resultieren folgende Schritte (in dieser Reihenfolge), um erfolgreich zu interpolieren:
1. Einfügen zusätzlicher Stützpunkte im Darstellungsraum, z.B. durch minimieren der Summe der (n-ten) Differenzenquadrate, separat in den Punktkomponenten.
2. Berechnung des Faktors pot nach der Minimalbedingung, separat für die einzelnen Punktkomponenten.
3. Berechnung einzelner Faktoren pot[k], um die Minimalbedingung besser zu erfüllen.
Nach diesen drei Schritte kann man sehen, wie gut (oder schlecht) die Interpolation(sfunktion) zu 15 gegebenen Punkten hier eine Lemniskate reproduziert.

   Interpolation einer ungeordneten, schlichten Punktmenge
Bei der Interpolation einer ungeordneten, schlichten Punktmenge soll eine nachträgliche Umordnung der Argumente vermieden werden, weil
  1. das Interpolationsergebnis von der gewählten Anordnung der Argumente abhängig sein kann,
  2. eine sinnvolle Anordnung der Argumente mit zunehmender Dimension schwieriger wird.
Schließlich soll die Punktmenge, d.h. die Funktion über der Argumentmenge, nur interpoliert werden. Da ist ein einfaches und übersichtliches Vorgehen durchaus erwünscht. Eine mögliche Methode wird z.B. in [1] beschrieben. Hier folgt nun die grundlegende Interpolationsfunktion:

        real*8 function yvonx()
        implicit none
        integer k,i,n
        real*8 w,v,u
        include 'commointeger4real8.h'
        w=0.d0
        do n=1,kz
         v=cy(n)
         u=0.d0
         do i=1,iz
          u=u+(x(n,i)-xx(i))**2
         end do
         u=dsqrt(u)
         v=v*dexp(-p*u)
         w=w+v
        end do
        yvonx=w
        return
        end

Wie genau verfahren wird, entnimmt man den Quelltexten einer FORTRAN-Anwendung unter Suse-Linux 12.1 :

Die FORTRAN-Anwendungen können kostenlos übernommen und ohne Gewährleistung für evtl. Schäden verwendet werden. Bei geeigneter Ausstattung des Betriebssystems sollten keine rechentechnischen Umstände entstehen. Als Anhaltspunkt für eine Verwendung dienen die beiliegenden Beispiele, zu denen jetzt einige Abbildungen folgen:
  1. Interpolation einer Funktion zweier Veränderlicher und einige Ausschnittvergrößerungen. Bildergalerie
  2. Interpolation einer Funktion mit drei Veränderlichen; die dritte Variable soll die Messzeit wiedergeben. D.h. eine Bildfolge gibt die Entwichlung der Funktion während einer Zeitspanne wieder. Bildergalerie
Die Beispiele findet man im Quelltext der FORTRAN-Anwendung vor. Sie sollen zu weiteren Anwendungen des Programms anregen.
Um z.B. die Neigungen der Funktion in ihrem Definitionsbereich zu erfassen, wird die Interpolation in zwei Schritten durchgeführt:
1. Approximation der Funktion in ihrem Definitionsbereich.
2. Interpolation der Differenzfunktion zur approximierenden Funktion im Definitionsbereich. Vergleich
Um die geeignete Ordnung der Approximationspolynome zu bestimmen, werden die jeweiligen Höhenliniendarstellungen der Approximationsfunktion und der darauf fußenden Interpolationsfunktion gegeben.

Allgemeiner können die Potenzwerte bei exp(-p*r) in Abhängigkeit vom betrachteten k-ten Messwert y auch variabel angenommen werden. Z.B. exp(-y(k)/(1+|y(k)|/p). Dann kommt in einem Beispiel mit 2000 Messpunkten folgende Reliefdarstellung zustande.

[1] Interpolation ungeordneter, schlichter Punktmengen mit der "Methode der reziproken Radien"
  H.Thielcke, ZAMM 1995
  Zeitschrift für Angewandte Mathematik und Mechanik
  AKADEMIE-VERLAG Berlin